题目内容
已知函数f(x)=x-alnx(a∈R).
(1)当a=2时,求曲线y=f(x)在点A(1,f(1))处的切线方程;
(2)求函数f(x)的极值.
[解析] 函数f(x)的定义域为(0,+∞),
f ′(x)=1-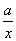 .
.
(1)当a=2时,f(x)=x-2lnx,f ′(x)=1-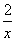 (x>0),
(x>0),
因而f(1)=1,f ′(1)=-1,
所以曲线y=f(x)在点A(1,f(1))处的切线方程为
y-1=-(x-1),
即x+y-2=0.
(2)由f ′(x)=1-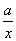 =
=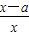 ,x>0知:
,x>0知:
①当a≤0时,f ′(x)>0,函数f(x)为(0,+∞)上的增函数,函数f(x)无极值;
②当a>0时,由f ′(x)=0,解得x=a.
又当x∈(0,a)时,f ′(x)<0;
当x∈(a,+∞)时,f ′(x)>0,
从而函数f(x)在x=a处取得极小值,
且极小值为f(a)=a-alna,无极大值.
综上,当a≤0时,函数f(x)无极值;
当a>0时,函数f(x)在x=a处取得极小值a-alna,无极大值.

练习册系列答案
相关题目
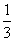 x3+
x3+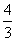 .
.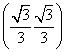 ,则a的取值范围是( )
,则a的取值范围是( )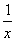 在(
在(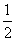 ,+∞)是增函数,则a的取值范围是( )
,+∞)是增函数,则a的取值范围是( )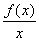 在区间(1,+∞)上一定( )
在区间(1,+∞)上一定( )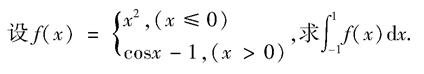
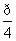 ,
,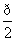 )上是增加的
)上是增加的