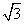题目内容
函数f(x)=x2-2ax+a在区间(-∞,1)上有最小值,则函数g(x)=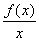 在区间(1,+∞)上一定( )
在区间(1,+∞)上一定( )
A.有最小值 B.有最大值
C.是减少的 D.是增加的
D
[解析] ∵f(x)=x2-2ax+a在区间(-∞,1)上有最小值,∴a<1.
∴g(x)=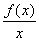 =x+
=x+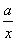 -2a,
-2a,
则g′(x)=1-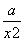 =
=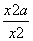 .
.
∵x∈(1,+∞),a<1,∴x2-a>0,即g′(x)>0.
∴g(x)在(1,+∞)上是增加的.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
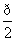 时,其导函数的值为________.
时,其导函数的值为________.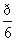 ≤x<
≤x<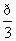 ,cosx=
,cosx=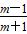 ,则m的取值范围是( )
,则m的取值范围是( )