题目内容
已知曲线y=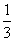 x3+
x3+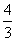 .
.
(1)求曲线在点P(2,4)处的切线方程;
(2)求曲线过点P(2,4)的切线方程.
[分析] (1)在点P处的切线以点P为切点.
(2)过点P的切线,点P不一定是切点,需要设出切点坐标.
(1)∵y′=x2,
∴在点P(2,4)处的切线的斜率k=y′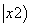 =4.
=4.
∴曲线在点P(2,4)处的切线方程为y-4=4(x-2),
即4x-y-4=0.
(2)设曲线y=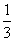 x3+
x3+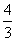 与过点P(2,4)的切线相切于点
与过点P(2,4)的切线相切于点
A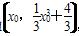 ,
,
则切线的斜率k=y′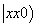 =x
=x .
.
∴切线方程为y-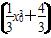 =x
=x (x-x0),
(x-x0),
即y=x ·x-
·x- x
x +
+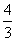 .
.
∵点P(2,4)在切线上,∴4=2x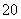 -
- x
x +
+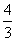 ,
,
即x -3x
-3x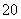 +4=0.∴x
+4=0.∴x +x
+x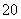 -4x
-4x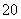 +4=0.
+4=0.
∴x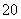 (x0+1)-4(x0+1)(x0-1)=0.
(x0+1)-4(x0+1)(x0-1)=0.
∴(x0+1)(x0-2)2=0,解得x0=-1或x0=2.
故所求的切线方程为4x-y-4=0或x-y+2=0.

练习册系列答案
相关题目
 时,其导函数的值为________.
时,其导函数的值为________.