题目内容
函数y=f(x)为定义在R上的减函数,函数y=f(x-1)的图象关于点(1,0)对称,x,y满足不等式f(x2-2x)+f(y2-2y)≥0,则当1≤x≤4时,
的取值范围为( )
| y |
| x |
| A、[12,+∞) | ||||
| B、[0,3] | ||||
C、[1-
| ||||
D、(-∞,1-
|
考点:简单线性规划
专题:数形结合
分析:根据函数y=f(x-1)的图象关于点(1,0)对称,可知函数是奇函数,再利用在R上的减函数,转化为具体的不等式,故可解.
解答:
解:根据函数y=f(x-1)的图象关于点(1,0)对称,
可知函数f(x)是奇函数,
∴由f(x2-2x)+f(y2-2y)≥0,得f(x2-2x)≥-f(-2y+y2)=f(2y-y2),
∵在R上的减函数y=f(x),
∴x2-2x≤2y-y2,
即(x-1)2+(y-1)2≤2,
又∵1≤x≤4,
平面区域如图所示.
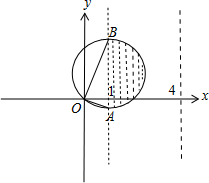
由图求得A(1,1-
),B(1,1+
).
∴
的取值范围为[1-
,1+
].
故选:C.
可知函数f(x)是奇函数,
∴由f(x2-2x)+f(y2-2y)≥0,得f(x2-2x)≥-f(-2y+y2)=f(2y-y2),
∵在R上的减函数y=f(x),
∴x2-2x≤2y-y2,
即(x-1)2+(y-1)2≤2,
又∵1≤x≤4,
平面区域如图所示.

由图求得A(1,1-
| 2 |
| 2 |
∴
| y |
| x |
| 2 |
| 2 |
故选:C.
点评:本题综合考查了函数的对称性、单调性、线性规划的可行域及其最值、数形结合的解题思想方法,考查了推理能力和计算能力,属于中档题.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
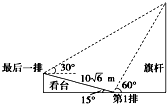 某校运动会开幕式上举行升旗仪式,在坡度为15°的看台上,同一列上的第一排和最后一排测得旗杆顶部的仰角分别为60°和30°,第一排和最后一排的距离为10
某校运动会开幕式上举行升旗仪式,在坡度为15°的看台上,同一列上的第一排和最后一排测得旗杆顶部的仰角分别为60°和30°,第一排和最后一排的距离为10| 6 |
| A、10 m | ||
| B、30 m | ||
C、10
| ||
D、10
|
已知函数f(x)=ln|x|+x2,则下列各式一定成立的是( )
| A、f(-7)<f(6) |
| B、f(-3)>f(2) |
| C、f(-1)>f(3) |
| D、f(-e)<f(-2) |
下列给出的赋值语句中正确的是( )
| A、3=A | B、x=-x |
| C、B=A=2 | D、x+y=0 |
若0<x<y<1,则( )
| A、3y<3x | ||||
B、(
| ||||
| C、logx3<logy3 | ||||
D、x-
|
设变量x、y满足约束条件
,则z=2x+3y的最大值为( )
|
| A、18 | B、2 | C、3 | D、0 |
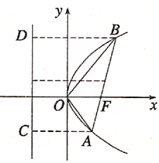 过抛物线y2=2px的焦点F的一条直线与它交于两点A(x1,y1),B(x2,y2),且直线AB的倾斜角为α,则以下正确的有:
过抛物线y2=2px的焦点F的一条直线与它交于两点A(x1,y1),B(x2,y2),且直线AB的倾斜角为α,则以下正确的有:


