��Ŀ����
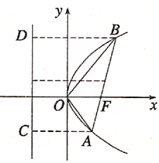 ��������y2=2px�Ľ���F��һ��ֱ��������������A��x1��y1����B��x2��y2������ֱ��AB����б��Ϊ������������ȷ���У�
��������y2=2px�Ľ���F��һ��ֱ��������������A��x1��y1����B��x2��y2������ֱ��AB����б��Ϊ������������ȷ���У���1��y1y2=-p2��x1x2=
| p2 |
| 4 |
��2��|AB|=x1+x2+p��
��3��S��AOB=
| 2�� |
| sin2�� |
��4��|AF|=
| p |
| 1-cos�� |
��5��
| 1 |
| |AF| |
| 1 |
| |BF| |
| 2 |
| p |
��6��|BF|=
| p |
| 1+cos�� |
��7����ABΪֱ����Բ�������ߵ����ཻ��
���㣺���������ж���Ӧ��,�����ߵļ�����
ר�⣺�Ķ���,Բ���ߵĶ��塢�����뷽��
��������1����AB��x=
��y=k��x-
�������������߷��̣���Τ�ﶨ�������ɵõ���
��2���������ߵĶ���ɵã�
�������ߵĶ���ɵ�BF=BD=p+BFcos������|BF|=
��ͬ���ɵ�|AF|=
�����жϣ�4������5������6����
��3��S��AOB=
��
����BFsin��+AFsin����������AF��BF���ɵõ���
��7������AB���е㵽�ߵľ������AC��BD�ĺ͵�һ�룬�������ߵĶ��壬�����жϣ�
| p |
| 2 |
| p |
| 2 |
��2���������ߵĶ���ɵã�
�������ߵĶ���ɵ�BF=BD=p+BFcos������|BF|=
| P |
| 1-cos�� |
| p |
| 1+cos�� |
��3��S��AOB=
| 1 |
| 2 |
| p |
| 2 |
��7������AB���е㵽�ߵľ������AC��BD�ĺ͵�һ�룬�������ߵĶ��壬�����жϣ�
���
�⣺��1����AB��x=
��y=k��x-
������x=
��
��y2=p2��y1y2=-p2��x1x2=
��
��y=k��x-
���������߷��̣��õ�k2x2-��kp+2p��x+
=0��
��x1x2=
��y1y2=-
=-p2���ʣ�1���ԣ�
��2���������ߵĶ���ɵã�|AB|=|AF|+|BF|=x1+x2+p���ʣ�2���ԣ�
��3��S��AOB=
��
����BFsin��+AFsin����=
��
+
��=
•
=
���ʣ�3������
�������ߵĶ���ɵ�BF=BD=p+BFcos����
��|BF|=
��ͬ���ɵ�|AF|=
���ʣ�4������6������ȷ��
��
+
=
+
=
���ʣ�5���ԣ�
��7������AB���е㵽�ߵľ������AC��BD�ĺ͵�һ�룬�������ߵĶ��壬��ΪAB��һ�룬����ABΪֱ����Բ�������ߵ������У��ʣ�7������
�ʴ�Ϊ����1����2����5����
| p |
| 2 |
| p |
| 2 |
| p |
| 2 |
��y2=p2��y1y2=-p2��x1x2=
| p2 |
| 4 |
��y=k��x-
| p |
| 2 |
| k2p2 |
| 4 |

��x1x2=
| p2 |
| 4 |
4p2•
|
��2���������ߵĶ���ɵã�|AB|=|AF|+|BF|=x1+x2+p���ʣ�2���ԣ�
��3��S��AOB=
| 1 |
| 2 |
| p |
| 2 |
| psin�� |
| 4 |
| P |
| 1-cos�� |
| p |
| 1+cos�� |
| 2p |
| sin2�� |
| psin�� |
| 4 |
| p2 |
| 2sin�� |
�������ߵĶ���ɵ�BF=BD=p+BFcos����
��|BF|=
| P |
| 1-cos�� |
| p |
| 1+cos�� |
��
| 1 |
| |AF| |
| 1 |
| |BF| |
| 1-cos�� |
| p |
| 1+cos�� |
| p |
| 2 |
| p |
��7������AB���е㵽�ߵľ������AC��BD�ĺ͵�һ�룬�������ߵĶ��壬��ΪAB��һ�룬����ABΪֱ����Բ�������ߵ������У��ʣ�7������
�ʴ�Ϊ����1����2����5����
���������⿼�������ߵĶ��塢���̺����ʣ���������ֱ�߷��̺������߷��̣�����Τ�ﶨ����⣬����ƽ�漸��֪ʶ�������е��⣮

��ϰ��ϵ�д�
 ��ĩ��ϰ���ϵ�д�
��ĩ��ϰ���ϵ�д� ����ѧ�䵥Ԫ������ĩר����100��ϵ�д�
����ѧ�䵥Ԫ������ĩר����100��ϵ�д� �Ƹ�360�ȶ����ܾ�ϵ�д�
�Ƹ�360�ȶ����ܾ�ϵ�д� ���⿼����Ԫ���Ծ�ϵ�д�
���⿼����Ԫ���Ծ�ϵ�д� ��У���˳�̾�ϵ�д�
��У���˳�̾�ϵ�д�
�����Ŀ
����y=f��x��Ϊ������R�ϵļ�����������y=f��x-1����ͼ����ڵ㣨1��0���Գƣ�x��y���㲻��ʽf��x2-2x��+f��y2-2y����0����1��x��4ʱ��
��ȡֵ��ΧΪ��������
| y |
| x |
| A��[12��+�ޣ� | ||||
| B��[0��3] | ||||
C��[1-
| ||||
D����-�ޣ�1-
|
