题目内容
函数f(x)=lnx-3+x的零点为x1,g(x)=ex-3+x的零点为x2,则x1+x2等于( )
| A、2 | B、3 | C、6 | D、1 |
考点:函数的零点
专题:函数的性质及应用
分析:因为f(x)的零点就是方程ex+x-3=0的根,同理g(x)的零点就是lnx+x-3=0的根,方程ex+x-3=0的根,就是y=ex与直线y=3-x的交点横坐标;
方程lnx+x-3=0的根,就是y=lnx与直线y=3-x的交点的横坐标,而y=ex与y=lnx互为反函数,其图象关于y=x对称,且直线y=3-x与直线y=x垂直,结合图象,可以得到所求.
方程lnx+x-3=0的根,就是y=lnx与直线y=3-x的交点的横坐标,而y=ex与y=lnx互为反函数,其图象关于y=x对称,且直线y=3-x与直线y=x垂直,结合图象,可以得到所求.
解答:
解:∵函数f(x)的零点就是方程ex+x-3=0的根,同理g(x)的零点就是lnx+x-3=0的根,
并且方程ex+x-3=0的根,就是y=ex与直线y=3-x的交点横坐标;
方程lnx+x-3=0的根,就是y=lnx与直线y=3-x的交点的横坐标,
而y=ex与y=lnx互为反函数,它们的图象关于y=x对称,且直线y=3-x与直线y=x垂直,
所以x1+x2=3;
故选B.
并且方程ex+x-3=0的根,就是y=ex与直线y=3-x的交点横坐标;
方程lnx+x-3=0的根,就是y=lnx与直线y=3-x的交点的横坐标,
而y=ex与y=lnx互为反函数,它们的图象关于y=x对称,且直线y=3-x与直线y=x垂直,
所以x1+x2=3;
故选B.
点评:本题考查了函数的零点;关键时将函数的零点与方程的根联系,结合图象得到交点的位置关系解答.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图是正方体的平面展开图,则在这个正方体中:
如图是正方体的平面展开图,则在这个正方体中:①BM与ED异面; ②CN∥BE;
③CN与BF成60°角; ④DM⊥BN.
以上四个命题中,正确的命题序号是( )
| A、①②③ | B、①②④ |
| C、①③④ | D、①②③④ |
函数y=
(0<φ<
)的图象如图,则( )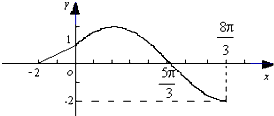
|
| π |
| 2 |

A、k=
| ||||||
B、k=
| ||||||
C、k=-
| ||||||
D、k=-2,ω=2,φ=
|