Question

8．一个几何体的三视图如图所示，该几何体外接球的表面积为（　　）

• A． 8π
• B． $\frac{25}{2}π$
• C． 12π
• D． $\frac{41}{4}π$

Answer 1

分析 作出正方体ABCD-A₁B₁C₁D₁，取CC₁的中点为E，DD₁的中点为F，则四棱锥A₁-ABEF的三视图为直观图，设三角形A₁AF的外心为O₁，三角形BEB₁的外心为O₁，该几何体外接球的球心为O₁O₂的中点，求出几何体外接球的半径，即可求出该几何体外接球的表面积．

解答 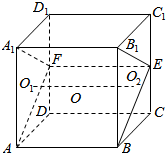解：作出正方体ABCD-A₁B₁C₁D₁，取CC₁的中点为E，DD₁的中点为F，则四棱锥A₁-ABEF的三视图为直观图，
设三角形A₁AF的外心为O₁，三角形BEB₁的外心为O₂，该几何体外接球的球心为O₁O₂的中点，
△A₁AF中，A₁A=2，AF=A₁F=$\sqrt{5}$，∴cos∠A₁FA=$\frac{5+5-4}{2×\sqrt{5}×\sqrt{5}}$=$\frac{3}{5}$，
∴sin∠A₁FA=$\frac{4}{5}$，
∴2R=$\frac{2}{\frac{4}{5}}$=$\frac{5}{2}$，
∴R=$\frac{5}{4}$，
∴几何体外接球的半径为$\sqrt{\frac{25}{16}+1}$=$\frac{\sqrt{41}}{4}$
∴几何体外接球的表面积为4$π•（\frac{\sqrt{41}}{4}）^{2}$=$\frac{41}{4}$π．
故选：D．

点评 本题考查三视图，考查几何体外接球的表面积，确定直观图的形状是关键．