题目内容
已知动点M到点A(2,0)的距离是它到点B(8,0)的距离的一半;直线l的方程为y-1=k(x+1).
(1)求M的轨迹方程;
(2)判断l与M的轨迹的位置关系,若相交求出最短的弦长;
(3)设l与M的轨迹相交于A、B两点,是否存在k使得OA⊥OB?若存在求出k;若不存在,请给予证明.
(1)求M的轨迹方程;
(2)判断l与M的轨迹的位置关系,若相交求出最短的弦长;
(3)设l与M的轨迹相交于A、B两点,是否存在k使得OA⊥OB?若存在求出k;若不存在,请给予证明.
考点:轨迹方程,直线与圆的位置关系
专题:综合题,直线与圆
分析:(1)利用动点M到点A(2,0)的距离是它到点B(8,0)的距离的一半,建立方程,化简即可求M的轨迹方程;
(2)直线过圆内的点B(-1,1),故相交,求出|OB|,即可求出最短的弦长;
(3)若OA⊥OB,则圆心到直线的距离为2
,建立方程可得结论.
(2)直线过圆内的点B(-1,1),故相交,求出|OB|,即可求出最短的弦长;
(3)若OA⊥OB,则圆心到直线的距离为2
| 2 |
解答:
解:(1)设动点M(x,y)为轨迹上任意一点,则点M的轨迹就是集合
P={M||MA|=
|MB|}.
由两点距离公式,点M适合的条件可表示为
=
,
平方后再整理,得 x2+y2=16. 可以验证,这就是动点M的轨迹方程.
(2)直线过圆内的点B(-1,1),故相交;
∵OB=
,r=4,∴最短弦长,2
=2
.
(3)若OA⊥OB,则圆心到直线的距离为2
,
∴
=2
,
∴7k2-2k+7=0,
方程无解,∴不存在
P={M||MA|=
| 1 |
| 2 |
由两点距离公式,点M适合的条件可表示为
| (x-2)2+y2 |
| 1 |
| 2 |
| (x-8)2+y2 |
平方后再整理,得 x2+y2=16. 可以验证,这就是动点M的轨迹方程.
(2)直线过圆内的点B(-1,1),故相交;
∵OB=
| 2 |
| 16-2 |
| 14 |
(3)若OA⊥OB,则圆心到直线的距离为2
| 2 |
∴
| |k+1| | ||
|
| 2 |
∴7k2-2k+7=0,
方程无解,∴不存在
点评:本题考查轨迹方程,考查直线与圆的位置关系,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
下列函数在区间(0,+∞)上单调递减的是( )
| A、y=-x2+8x+9 | ||
| B、y=10x | ||
| C、y=cosx | ||
D、y=
|
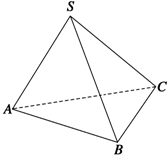 如图所示,在三棱锥S-ABC中,SA⊥SB,SB⊥SC,SA⊥SC,且SA、SB、SC和底面ABC所成的角分别为a1、a2、a3,三侧面△SBC、△SAC、△SAB的面积分别为S1、S2、S3,类比三角形中的正弦定理,给出空间情形的一个猜想.
如图所示,在三棱锥S-ABC中,SA⊥SB,SB⊥SC,SA⊥SC,且SA、SB、SC和底面ABC所成的角分别为a1、a2、a3,三侧面△SBC、△SAC、△SAB的面积分别为S1、S2、S3,类比三角形中的正弦定理,给出空间情形的一个猜想.