题目内容
某市现行出租车收费标准如下:不考虑其他因素下,每次运行起步价为(包括燃油附加费在内)4里内5元(不含4里),满4里后的续程运行价为每里跳表计费1元.
(1)若某乘客坐出租车行驶了[n,n+1)(n∈N*,n≥4)里,他应付给司机的费用(元)记作an,求an(n≥4)的表达式.
(2)令bn=
,构造函数f(n)=
+
+…+
,n∈N*,n≥2,若对任意,都有恒成立,试求k的取值范围.
(1)若某乘客坐出租车行驶了[n,n+1)(n∈N*,n≥4)里,他应付给司机的费用(元)记作an,求an(n≥4)的表达式.
(2)令bn=
|
| 1 |
| n-2+b1 |
| 1 |
| n-2+b2 |
| 1 |
| n-2+bn |
考点:数列的应用
专题:综合题,等差数列与等比数列
分析:(1)a4=6,n≥4时,{an}构成等差数列,公差为1,即可求an(n≥4)的表达式.
(2)bn=n+2,求出f(n),再利用作差法,确定f(n)随n的增大而增大,可得其最小值,即可求k的取值范围.
(2)bn=n+2,求出f(n),再利用作差法,确定f(n)随n的增大而增大,可得其最小值,即可求k的取值范围.
解答:
解:(1)易知a4=6,n≥4时,{an}构成等差数列,公差为1,----(2分)
故当n∈N*,n≥4时,an=a4+(n-4)×1=n+2------(5分)
(2)由已知{bn}构成等差数列,即bn=n+2,n∈N*-------(6分)
故f(n)=
+
+…+
,-----------(8分)
f(n+1)=
+
+…+
+
+
,
所以f(n+1)-f(n)=
+
-
>
+
-
=0-------(10分)
故f(n)随n的增大而增大,其最小值为f(2)=
+
=
,
由已知,应有k≤
,即 k∈(-∞,
]-----(13分)
故当n∈N*,n≥4时,an=a4+(n-4)×1=n+2------(5分)
(2)由已知{bn}构成等差数列,即bn=n+2,n∈N*-------(6分)
故f(n)=
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| n+n |
f(n+1)=
| 1 |
| n+2 |
| 1 |
| n+3 |
| 1 |
| 2n |
| 1 |
| 2n+1 |
| 1 |
| 2n+2 |
所以f(n+1)-f(n)=
| 1 |
| 2n+1 |
| 1 |
| 2n+2 |
| 1 |
| n+1 |
| 1 |
| 2n+2 |
| 1 |
| 2n+2 |
| 1 |
| n+1 |
故f(n)随n的增大而增大,其最小值为f(2)=
| 1 |
| 3 |
| 1 |
| 4 |
| 7 |
| 12 |
由已知,应有k≤
| 7 |
| 12 |
| 7 |
| 12 |
点评:本题考查数列的应用,考查数列的单调性,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在具有如图所示的正视图和俯视图的几何体中,体积最小的几何体的表面积为 ( )
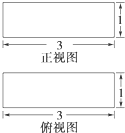

| A、13 | ||
B、7+3
| ||
C、
| ||
| D、14 |
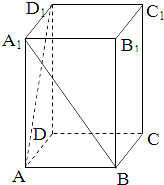 在长方体ABCD-A1B1C1D1中,已知DA=DC=4,DD1=3,求异面直线A1B与D1A所成角的余弦值( )
在长方体ABCD-A1B1C1D1中,已知DA=DC=4,DD1=3,求异面直线A1B与D1A所成角的余弦值( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,简单组合体ABCDPE,其底面ABCD是边长为2的正方形,PD⊥平面ABCD,EC∥PD,且PD=2EC=2.
如图,简单组合体ABCDPE,其底面ABCD是边长为2的正方形,PD⊥平面ABCD,EC∥PD,且PD=2EC=2.