题目内容
 如图,PA⊥平面ABCD,四边形ABCD是矩形,PA=AD=a,M、N分别是AB、PC的中点.
如图,PA⊥平面ABCD,四边形ABCD是矩形,PA=AD=a,M、N分别是AB、PC的中点.(Ⅰ)求平面PCD与平面ABCD所成二面角的大小;
(Ⅱ)求证:平面MND⊥平面PCD;
(Ⅲ)当AB的长度变化时,求异面直线PC与AD所成角的取值范围.
考点:异面直线及其所成的角,平面与平面垂直的判定,二面角的平面角及求法
专题:综合题,空间位置关系与距离,空间角
分析:(Ⅰ)由题设条件及几何体的直观图可证得∠PDA是平面PCD与平面ABCD所成二面角的平面角,在Rt△PAD中,求出此角的值即可得到二面角的大小;
(Ⅱ)观察图形,取PD中点E,连接AE,EN,又M,N分别是AB,PC的中点可证得四边形AMNE是平行四边形,得出MN∥AE,再证明AE⊥平面PCD得到MN⊥平面PCD,即可证明平面MND⊥平面PCD;
(Ⅲ)求异面直线所成的角得先作角,由图形及题设条件知∠PCB为异面直线PC,AD所成的角,在三角形PCB中解此角即可
(Ⅱ)观察图形,取PD中点E,连接AE,EN,又M,N分别是AB,PC的中点可证得四边形AMNE是平行四边形,得出MN∥AE,再证明AE⊥平面PCD得到MN⊥平面PCD,即可证明平面MND⊥平面PCD;
(Ⅲ)求异面直线所成的角得先作角,由图形及题设条件知∠PCB为异面直线PC,AD所成的角,在三角形PCB中解此角即可
解答:
(Ⅰ)解:PA⊥平面ABCD,CD⊥AD,∴PD⊥CD.
故∠PDA是平面PCD与平面ABCD所成二面角的平面角.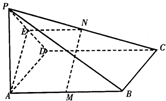
在Rt△PAD中,PA⊥AD,PA=AD,∴∠PDA=45°.…(3分)
(Ⅱ)证明:如图,取PD中点E,连接AE,EN,又M,N分别是AB,PC的中点,
∴EN∥
CD∥
AB,
∴AMNE是平行四边形,
∴MN∥AE.
在等腰Rt△PAD中,AE是斜边的中线,∴AE⊥PD.
由PA⊥平面ABCD,四边形ABCD是矩形,可推出CD⊥PD
又CD⊥AD,AD∩PD=D
∴CD⊥平面PAD,∴CD⊥AE,
又PD∩CD=D,∴AE⊥平面PCD,
∴MN⊥平面PCD,
∵MN?平面MND,
∴平面MND⊥平面PCD…(7分)
(Ⅲ)解:∵AD∥BC,∴∠PCB为异面直线PC,AD所成的角.
由三垂线定理知PB⊥BC,设AB=x(x>0).
∴tan∠PCB=
.
又∵
∈(0,+∞),∴tan∠PCB∈(1,+∞).
又∠PCB为锐角,∴∠PCB∈(
,
),
即异面直线PC,AD所成的角的范围为(
,
).…(12分)
故∠PDA是平面PCD与平面ABCD所成二面角的平面角.

在Rt△PAD中,PA⊥AD,PA=AD,∴∠PDA=45°.…(3分)
(Ⅱ)证明:如图,取PD中点E,连接AE,EN,又M,N分别是AB,PC的中点,
∴EN∥
| 1 |
| 2 |
| 1 |
| 2 |
∴AMNE是平行四边形,
∴MN∥AE.
在等腰Rt△PAD中,AE是斜边的中线,∴AE⊥PD.
由PA⊥平面ABCD,四边形ABCD是矩形,可推出CD⊥PD
又CD⊥AD,AD∩PD=D
∴CD⊥平面PAD,∴CD⊥AE,
又PD∩CD=D,∴AE⊥平面PCD,
∴MN⊥平面PCD,
∵MN?平面MND,
∴平面MND⊥平面PCD…(7分)
(Ⅲ)解:∵AD∥BC,∴∠PCB为异面直线PC,AD所成的角.
由三垂线定理知PB⊥BC,设AB=x(x>0).
∴tan∠PCB=
1+(
|
又∵
| x |
| a |
又∠PCB为锐角,∴∠PCB∈(
| π |
| 4 |
| π |
| 2 |
即异面直线PC,AD所成的角的范围为(
| π |
| 4 |
| π |
| 2 |
点评:本题考查与二面角有关的立体几何综合题,解题的关键是熟练掌握二面角的求法,其步骤一般分为三步,作角,证角,求角,其中第二步证角易被忽略导致失分,解题时要注意解题的骤,本题中第二小问证明面面垂直,要注意正确使用判定定理,第三问中求异面直线所成的角,其作法也是要先作角,证角,求角,几何中求角的题其做题步骤基本上都分为此三步,做题后注意总结一下这个规律

练习册系列答案
相关题目
 某几何体的三视图如图所示,主视图和左视图是长为3,宽为2的矩形,俯视图是边长为2的正方形,则该几何体的体积为
某几何体的三视图如图所示,主视图和左视图是长为3,宽为2的矩形,俯视图是边长为2的正方形,则该几何体的体积为