题目内容
若1+sin2θ=3sinθcosθ,则tanθ= .
考点:三角函数的化简求值
专题:三角函数的求值
分析:通过同角三角函数的基本关系式化简已知表达式,然后求解方程即可.
解答:
解:由1+sin2θ=3sinθcosθ,
变形得2sin2θ+cos2θ-3sinθcosθ=0,
⇒(2sinθ-cosθ)(sinθ-cosθ)=0,
∴tanθ=
或1.
故答案为:1或
.
变形得2sin2θ+cos2θ-3sinθcosθ=0,
⇒(2sinθ-cosθ)(sinθ-cosθ)=0,
∴tanθ=
| 1 |
| 2 |
故答案为:1或
| 1 |
| 2 |
点评:本题考查三角函数化简求值,同角三角函数的基本关系式的应用,考查计算能力.

练习册系列答案
相关题目
学校计划利用周五下午第一、二、三节课举办语文、数学、英语、理综4科的专题讲座,每科一节课,每节至少有一科,且数学、理综不安排在同一节,则不同的安排方法共有( )
| A、36种 | B、30种 |
| C、24种 | D、6种 |
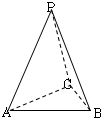 在三棱锥P-ABC中,已知PA=PB=PC=2,∠BPA=∠BPC=∠CPA=30°,一绳子从A点绕三棱锥侧面一圈回到点A的距离中,绳子最短距离是
在三棱锥P-ABC中,已知PA=PB=PC=2,∠BPA=∠BPC=∠CPA=30°,一绳子从A点绕三棱锥侧面一圈回到点A的距离中,绳子最短距离是