题目内容
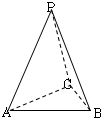 在三棱锥P-ABC中,已知PA=PB=PC=2,∠BPA=∠BPC=∠CPA=30°,一绳子从A点绕三棱锥侧面一圈回到点A的距离中,绳子最短距离是
在三棱锥P-ABC中,已知PA=PB=PC=2,∠BPA=∠BPC=∠CPA=30°,一绳子从A点绕三棱锥侧面一圈回到点A的距离中,绳子最短距离是考点:多面体和旋转体表面上的最短距离问题
专题:计算题,空间位置关系与距离
分析:将三棱锥的侧面展开,求一绳子从A点绕三棱锥侧面一圈回到点A的距离中,绳子最短距离,可转化为求AA1的长度,利用勾股定理即可得到答案.
解答:
解:设过点A作截面AEF与PB、PC侧棱分别交于E、F两点,将三棱锥由PA展开,则∠APA1=90°,
AA1为绳子从点A沿侧面到棱PB上的点E处,再到棱PC上的点F处,然后回到点A的最短距离,
∵PA=2,
∴由勾股定理可得AA1=
=2
.
故答案为:2
.
AA1为绳子从点A沿侧面到棱PB上的点E处,再到棱PC上的点F处,然后回到点A的最短距离,
∵PA=2,
∴由勾股定理可得AA1=
| 4+4 |
| 2 |
故答案为:2
| 2 |
点评:本题考查的知识点是多面体和旋转体表面上的最短距离问题,其中将三棱锥的侧面展开,将空间问题转化为平面上两点间距离问题,是解答本题的关键.

练习册系列答案
相关题目
由小到大排列的一组数据:x1,x2,x3,x4,x5,其中每个数据都小于-2,则样本2,-x1,x2,x3,-x4,x5的中位数可以表示为( )
A、
| ||
B、
| ||
C、
| ||
D、
|