题目内容
某工厂生产甲、乙两种产品,每生产1只甲产品需要A原料3克,B原料4克,C原料4克;每生产1只乙产品需要A原料2克,B原料5克,C原料6克;根据限额,每天A原料不超过120克,B原料不超过100克,C原料不超过240克;已知甲产品每只可获利20元,乙产品每只可获利10元,该工厂每天生产这两种产品各多少只,才能获利最大?
考点:简单线性规划的应用,简单线性规划
专题:不等式的解法及应用
分析:先设每天生产甲产品为x只,乙产品为y只,列出约束条件,再根据约束条件画出可行域,设z=20x+10y,再利用z的几何意义求最值,只需求出直线z=20x+10y过可行域内的A点时,从而得到z值即可.
解答:
解:设每天生产甲产品为x只,乙产品为y只,则有:
,
目标函数z=20x+10y,
作出可行域如图所示:
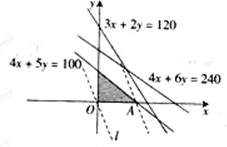
由z=20x+10y知y=-2x+
,
作出直线系y=-2x+
,
当直线经过可行域上的点A时,纵截距达到最大,
即z达到最大.
由
得A点坐标为(25,0)
∴甲产品生产25只.乙产品生产0只时,该企业可获得最大利润.
|
目标函数z=20x+10y,
作出可行域如图所示:

由z=20x+10y知y=-2x+
| z |
| 10 |
作出直线系y=-2x+
| z |
| 10 |
当直线经过可行域上的点A时,纵截距达到最大,
即z达到最大.
由
|
∴甲产品生产25只.乙产品生产0只时,该企业可获得最大利润.
点评:在解决线性规划的应用题时,其步骤为:①分析题目中相关量的关系,列出不等式组,即约束条件⇒②由约束条件画出可行域⇒③分析目标函数Z与直线截距之间的关系⇒④使用平移直线法求出最优解⇒⑤还原到现实问题中.

练习册系列答案
相关题目
下列结论中正确的个数是( )
①在△ABC中,若acosB=bcosA,则△ABC为等腰三角形
②若等差数列的通项公式为an=4n-21,则S5为最小值;
③当0<x<2时,函数f(x)=x(4-2x)的最大值为2
④垂直于同一个平面的两个平面互相平行.
①在△ABC中,若acosB=bcosA,则△ABC为等腰三角形
②若等差数列的通项公式为an=4n-21,则S5为最小值;
③当0<x<2时,函数f(x)=x(4-2x)的最大值为2
④垂直于同一个平面的两个平面互相平行.
| A、.1 | B、2 | C、.3 | D、4 |
已知E为不等式组
,表示区域内的一点,过点E的直线l与圆M:(x-1)2+y2=9相交于A,C两点,过点E与l垂直的直线交圆M于B、D两点,当AC取最小值时,四边形ABCD的面积为( )
|
| A、12 | ||
B、6
| ||
C、12
| ||
D、4
|
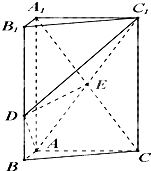 如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠BAC=90°,AB=2,AC=6,点D在线段BB1上,且BD=
如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠BAC=90°,AB=2,AC=6,点D在线段BB1上,且BD=
 对某同学的6次数学测试成绩(满分100分)进行统计,作出的茎叶图如图所
对某同学的6次数学测试成绩(满分100分)进行统计,作出的茎叶图如图所