题目内容
在△ABC中,a、b、c分别是三内角A、B、C的对边,A=75°,C=45°,b=1,则此三角形的最小边长为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:正弦定理
专题:解三角形
分析:先利用三角形内角和求得B,进而判断出最小的边,利用正弦定理求得其边长.
解答:
解:B=180°-A-C=60°,
∴c为最小的边,
由正弦定理得
=
,
∴c=
•sinC=
×
=
,
故选B.
∴c为最小的边,
由正弦定理得
| b |
| sinB |
| c |
| sinC |
∴c=
| b |
| sinB |
| 1 | ||||
|
| ||
| 2 |
| ||
| 3 |
故选B.
点评:本题主要考查了正弦定理的应用.注重了对三角函数基础公式的记忆和应用.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
已知3,a,13成等差数列,实数c,9,27成等比数列,则a+c的值是( )
| A、11 | B、12 | C、13 | D、14 |
已知集合M={(x,y)|y=3x+1}和集合N={(x,y)|y=x2+x+1},则M∩N=( )
| A、{0,2} |
| B、∅ |
| C、[1,+∞) |
| D、{(0,1),(2,7)} |
设x∈(0,π),则函数y=sinx+
的最小值是( )
| 1 |
| sinx |
| A、2 | ||
B、
| ||
C、
| ||
| D、3 |
已知集合A={x|(x+3)(x-2)≤0},B={x|-1<x≤3},则A∩B=( )
| A、[-3,0] |
| B、(-1,2] |
| C、[-3,3] |
| D、[-1,2] |
当你到一个红绿灯路口时,红灯的时间为30秒,黄灯的时间为5秒,绿灯的时间为45秒,那么你看到黄灯的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
使不等式
+
>1+
成立的正整数a的最大值是( )
| 3 |
| 8 |
| a |
| A、10 | B、11 | C、12 | D、13 |
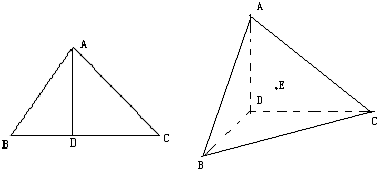 如图,∠ACB=45°,BC=6过A作AD⊥BC,垂足D在线段BC上且异于点B,沿AD将△ABD折起,组成三棱锥A-BCD,过点D作DE⊥平面ABC,且点E为三角形ABC的垂心.
如图,∠ACB=45°,BC=6过A作AD⊥BC,垂足D在线段BC上且异于点B,沿AD将△ABD折起,组成三棱锥A-BCD,过点D作DE⊥平面ABC,且点E为三角形ABC的垂心.