题目内容
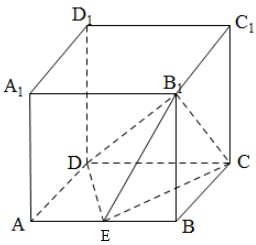
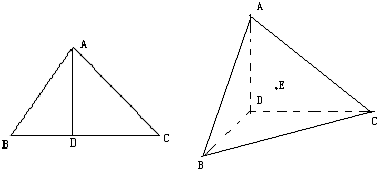 如图,∠ACB=45°,BC=6过A作AD⊥BC,垂足D在线段BC上且异于点B,沿AD将△ABD折起,组成三棱锥A-BCD,过点D作DE⊥平面ABC,且点E为三角形ABC的垂心.
如图,∠ACB=45°,BC=6过A作AD⊥BC,垂足D在线段BC上且异于点B,沿AD将△ABD折起,组成三棱锥A-BCD,过点D作DE⊥平面ABC,且点E为三角形ABC的垂心.(1)求证:△BDC为直角三角形.
(2)当BD的长为多少时,三棱锥A-BCD的体积最大?并求出其最大值.
考点:直线与平面垂直的性质,棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:(1)连接CE并延长,使CE∩AB=F,先证明出AB⊥CD和AD⊥DC,进而推断出CD⊥平面ABD,根据线面垂直的性质推断出CD⊥BD,即△BDC为直角三角形.
(2)设CD=x,表示出棱锥A-BCD体积的表达式,对其进行求导,令导函数等于0,求得x,把x代入体积表达式,求得体积的最大值.
(2)设CD=x,表示出棱锥A-BCD体积的表达式,对其进行求导,令导函数等于0,求得x,把x代入体积表达式,求得体积的最大值.
解答:
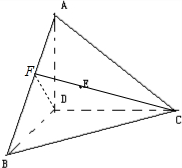 (1)证明:连接CE并延长,使CE∩AB=F,
(1)证明:连接CE并延长,使CE∩AB=F,
∵点E为垂心,
∴AB⊥CF,
∵DE⊥平面ABC,
∴AB⊥DF,
∴AB⊥平面CDF,
∵CD?平面CDF,
∴AB⊥CD,
∵AD⊥BD,AD⊥CD,
∴AD⊥平面BDC,
∵DC?平面BDC,
∴AD⊥DC,
∵AD?平面ABD,BD?平面ABD,AD∩BD=D,
∴CD⊥平面ABD,
∵BD?平面ABD,
∴CD⊥BD,即∠BDC=90°,
∴△BDC为直角三角形.
(2)设CD=x,所以AD=x,即三棱锥A-BCD的体积V=
x2(6-x),
V′=
(-3x2+12x)=-
x(x-4)
即当x=4时,三棱锥A-BCD的体积最大.Vmax=
.
 (1)证明:连接CE并延长,使CE∩AB=F,
(1)证明:连接CE并延长,使CE∩AB=F,∵点E为垂心,
∴AB⊥CF,
∵DE⊥平面ABC,
∴AB⊥DF,
∴AB⊥平面CDF,
∵CD?平面CDF,
∴AB⊥CD,
∵AD⊥BD,AD⊥CD,
∴AD⊥平面BDC,
∵DC?平面BDC,
∴AD⊥DC,
∵AD?平面ABD,BD?平面ABD,AD∩BD=D,
∴CD⊥平面ABD,
∵BD?平面ABD,
∴CD⊥BD,即∠BDC=90°,
∴△BDC为直角三角形.
(2)设CD=x,所以AD=x,即三棱锥A-BCD的体积V=
| 1 |
| 6 |
V′=
| 1 |
| 6 |
| 1 |
| 2 |
即当x=4时,三棱锥A-BCD的体积最大.Vmax=
| 16 |
| 3 |
点评:本题主要考查了线面垂直的判定和线面垂直的性质的应用,三棱锥体积的计算.考查了学生空间观察能力和运算能力.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
在△ABC中,a、b、c分别是三内角A、B、C的对边,A=75°,C=45°,b=1,则此三角形的最小边长为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知1,a1,a2,9四个实数成等差数列,1,b1,b2,b3,9五个数成等比数列,则b2(a2-a1)等于( )
| A、8 | ||
| B、-8 | ||
| C、±8 | ||
D、
|
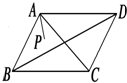
如图,点P等可能分布在菱形ABCD内,则
•
≤
|
|2的概率是( )
| AP |
| AC |
| 1 |
| 4 |
| AC |

A、
| ||
B、
| ||
C、
| ||
D、
|
如图所示的程序框图,其输出的结果是( )
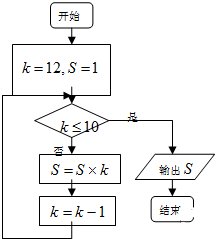

| A、11 | B、12 |
| C、131 | D、132 |
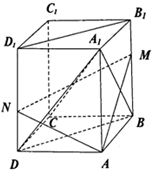 如图,长方体ABCD-A1B1C1D1中,点M,N分别在BB1,DD1上,且AM⊥A1B,AN⊥A1D.
如图,长方体ABCD-A1B1C1D1中,点M,N分别在BB1,DD1上,且AM⊥A1B,AN⊥A1D.