题目内容
使不等式
+
＞1+
成立的正整数a的最大值是（ ）
| 3 |
| 8 |
| a |
| A、10 | B、11 | C、12 | D、13 |
考点：不等式比较大小
专题：不等式的解法及应用
分析：本题利用两边平方法比较大小，然后找到最大值．
解答：
解：∵
+
＞1+
∴
＜
+
-1
∴a＜(
+
-1)2=12+2（2
-
-2
）＜13
故不等式
+
＞1+
成立的正整数a的最大值是12．
故选：C
| 3 |
| 8 |
| a |
∴
| a |
| 3 |
| 8 |
∴a＜(
| 3 |
| 8 |
| 6 |
| 3 |
| 2 |
故不等式
| 3 |
| 8 |
| a |
故选：C
点评：本题主要考查了比较大小的常用方法，两边平方法，属于基础题．
练习册系列答案
相关题目
已知i为虚数单位，如图中复平面内的点A表示复数z，则表示复数
的点是（ ）
| z |
| 1-i |
| A、M | B、N | C、P | D、Q |
在△ABC中，a、b、c分别是三内角A、B、C的对边，A=75°，C=45°，b=1，则此三角形的最小边长为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列各对函数中，相同的是（ ）
A、f（x）=
| ||||||||
| B、f（x）=lgx2，g（x）=2lgx | ||||||||
C、f（x）=
| ||||||||
D、f（μ）=
|
圆心在直线x+y-2=0上的圆的方程是（ ）
| A、（x+1）2+（y+1）2=4 |
| B、（x+1）2+（y-1）2=4 |
| C、（x-1）2+（y-1）2=4 |
| D、（x-1）2+（y+1）2=4 |
将角
表示为2kπ+α（k∈Z）的形式，则使|α|最小的角α是（ ）
| 19π |
| 5 |
A、-
| ||
B、
| ||
C、-
| ||
D、
|
已知1，a1，a2，9四个实数成等差数列，1，b1，b2，b3，9五个数成等比数列，则b2（a2-a1）等于（ ）
| A、8 | ||
| B、-8 | ||
| C、±8 | ||
D、
|
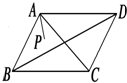
如图，点P等可能分布在菱形ABCD内，则
•
≤
|
|2的概率是（ ）
| AP |
| AC |
| 1 |
| 4 |
| AC |
A、
| ||
B、
| ||
C、
| ||
D、
|
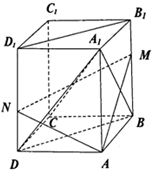如图，长方体ABCD-A1B1C1D1中，点M，N分别在BB1，DD1上，且AM⊥A1B，AN⊥A1D．