题目内容
已知集合M={(x,y)|y=3x+1}和集合N={(x,y)|y=x2+x+1},则M∩N=( )
| A、{0,2} |
| B、∅ |
| C、[1,+∞) |
| D、{(0,1),(2,7)} |
考点:交集及其运算
专题:集合
分析:M∩N={(x,y)|
}.
|
解答:
解:∵集合M={(x,y)|y=3x+1},
集合N={(x,y)|y=x2+x+1},
∴M∩N={(x,y)|
}
={(0,1),(2,7)}.
故选:D.
集合N={(x,y)|y=x2+x+1},
∴M∩N={(x,y)|
|
={(0,1),(2,7)}.
故选:D.
点评:本题考查交集的求法,解题时要认真审题,是基础题.

练习册系列答案
相关题目
已知i为虚数单位,如图中复平面内的点A表示复数z,则表示复数
的点是( )

| z |
| 1-i |

| A、M | B、N | C、P | D、Q |
已知tanα=2,tan(α-β)=-
,则tanβ等于( )
| 3 |
| 5 |
| A、13 | B、-13 | C、7 | D、-7 |
把函数y=sin(2x-
)的图象上的所有点向右平移
个单位,再把所有点的横坐标缩短到原来的一半,而把所有点的纵坐标伸长到原来的4倍,所得图象的表达式是 ( )
| π |
| 5 |
| π |
| 5 |
| A、y=4sin4x | ||
B、y=4sin(4x-
| ||
C、y=4sin(4x+
| ||
D、y=4sin(4x-
|
等差数列{an}中,d=-3,a7=10,则a1等于( )
| A、-39 | B、28 | C、39 | D、32 |
在△ABC中,a、b、c分别是三内角A、B、C的对边,A=75°,C=45°,b=1,则此三角形的最小边长为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列各对函数中,相同的是( )
A、f(x)=
| ||||||||
| B、f(x)=lgx2,g(x)=2lgx | ||||||||
C、f(x)=
| ||||||||
D、f(μ)=
|
如图,点P等可能分布在菱形ABCD内,则
•
≤
|
|2的概率是( )
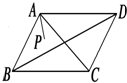
| AP |
| AC |
| 1 |
| 4 |
| AC |

A、
| ||
B、
| ||
C、
| ||
D、
|