题目内容
设x∈（0，π），则函数y=sinx+
的最小值是（ ）
| 1 |
| sinx |
| A、2 | ||
B、
| ||
C、
| ||
| D、3 |
考点：基本不等式
专题：计算题,不等式的解法及应用
分析：直接利用基本不等式即可求得．
解答：
解：∵x∈（0，π），∴sinx＞0，
∴y=sinx+
≥2
=2，
当且仅当sinx=
，即x=
时取等号，
∴函数y=sinx+
的最小值是2，
故选A．
∴y=sinx+
| 1 |
| sinx |
sinx•
|
当且仅当sinx=
| 1 |
| sinx |
| π |
| 2 |
∴函数y=sinx+
| 1 |
| sinx |
故选A．
点评：该题考查利用基本不等式求函数的最值，注意使用基本不等式求函数最值时的条件：一正、二定、三相等．
练习册系列答案
能力评价系列答案
唐印文化课时测评系列答案
相关题目
y=cosx（cosx+sinx）的值域是（ ）
| A、[-2，2] | ||||||||
B、[
| ||||||||
C、[
| ||||||||
D、[-
|
把函数y=sin（2x-
）的图象上的所有点向右平移
个单位，再把所有点的横坐标缩短到原来的一半，而把所有点的纵坐标伸长到原来的4倍，所得图象的表达式是 （ ）
| π |
| 5 |
| π |
| 5 |
| A、y=4sin4x | ||
B、y=4sin（4x-
| ||
C、y=4sin（4x+
| ||
D、y=4sin（4x-
|
边长分别为3，5，7的三角形的最大内角为（ ）
| A、150° | B、135° |
| C、120° | D、90° |
在△ABC中，a、b、c分别是三内角A、B、C的对边，A=75°，C=45°，b=1，则此三角形的最小边长为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
六个棱长为1的正方体在桌面上堆叠成一个几何体，该几何体的正视图与俯视图如图所示，则其左视图不可能为（ ）
圆心在直线x+y-2=0上的圆的方程是（ ）
| A、（x+1）2+（y+1）2=4 |
| B、（x+1）2+（y-1）2=4 |
| C、（x-1）2+（y-1）2=4 |
| D、（x-1）2+（y+1）2=4 |
如图所示的程序框图，其输出的结果是（ ）
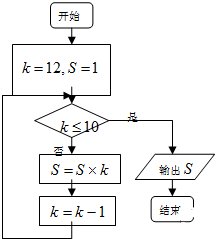
| A、11 | B、12 |
| C、131 | D、132 |