题目内容
5.已知函数$f(x)=\frac{1}{3}{x^3}+({a-6})x$,g(x)=-x2+lnx-1(Ⅰ)若a=2,求f(x)的单调区间;
(Ⅱ)对?x1,x2∈[1,+∞),都有f(x1)>g(x2),求实数a的取值范围.
分析 (1)利用导数列表判断
(2)利用导数求解函数最大值,最小值,转化为f(x)的最小值,g(x)的最大值比较即可,得出即$\frac{1}{3}{x^3}+(a-6)x>-2a>-\frac{1}{3}{x^2}-\frac{2}{x}+6$恒成立.
解答 解:(1)$f(x)=\frac{1}{3}{x^3}-4x{f^/}(x)={x^2}-4$
令f′(x)=0得x1=-2x2=2
| x | (-∞,-2) | (-2,2) | (2,+∞) |
| f′(x) | + | - | + |
| f(x) | ↑ | ↓ | ↑ |
(2)${g^/}(x)=-2x+\frac{1}{x}$若x∈[1,+∞)则g′(x)<0
∴g(x)在[1,+∞)上单调递减,g(x)的最大值为-2
要使f(x1)>g(x2)成立
即f(x)>-2,x∈[1,+∞)恒成立
即$\frac{1}{3}{x^3}+(a-6)x>-2a>-\frac{1}{3}{x^2}-\frac{2}{x}+6$恒成立
令$h(x)=-\frac{1}{3}{x^2}-\frac{2}{x}+6$求得它在[1,+∞)的最大值为$6-\root{3}{9}$
∴$a>6-\root{3}{9}$
点评 本题综合考查了运用导数解决函数单调性,的问题,关键判断最值,得出恒成立的条件.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
4.已知f(x)=$\left\{\begin{array}{l}-{x^2}+3x(x<2)\\ 2x-1(x≥2)\end{array}$,则f(-1)+f(4)的值为( )
| A. | -7 | B. | -8 | C. | 3 | D. | 4 |
10.已知函数f(x)=(2ax-lnx)x有两个极值点,则实数a的取值范围是( )
| A. | (0,$\frac{1}{4}$) | B. | (0,$\frac{1}{2}$) | C. | (0,1) | D. | (0,+∞) |
17.一个几何体的三视图如图所示,则三视图表示的几何体的体积最大为( )
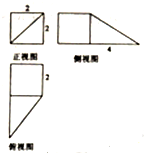

| A. | $\frac{40}{3}$ | B. | 40 | C. | $\frac{20}{3}$ | D. | 20 |
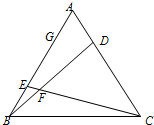 如图,正△ABC中,点D在边AC上,E,G在边AB上,且AB=3AG=6,AD=λAC,AE=(1-λ)AB,(0<λ<1),BD,CE相交于点F
如图,正△ABC中,点D在边AC上,E,G在边AB上,且AB=3AG=6,AD=λAC,AE=(1-λ)AB,(0<λ<1),BD,CE相交于点F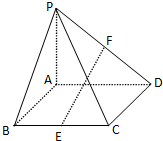 如图,在四棱锥P-ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,点E,F分别为BC、PD的中点,若PA=AD=4,AB=2.
如图,在四棱锥P-ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,点E,F分别为BC、PD的中点,若PA=AD=4,AB=2.