题目内容
6.过抛物线y=x2的焦点F作一直线交抛物线于M(x1,y1)、N(x2,y2)两点,如果y1+y2=1,则线段MN的中点到准线的距离等于( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
分析 由题意,y1+y2=1,则线段MN的中点纵坐标为$\frac{1}{2}$,即可求出线段MN的中点到准线的距离.
解答 解:由题意,y1+y2=1,则线段MN的中点纵坐标为$\frac{1}{2}$,
∴线段MN的中点到准线的距离等于$\frac{1}{4}+\frac{1}{2}$=$\frac{3}{4}$,
故选C.
点评 本题主要考查抛物线的基本性质,考查学生的计算能力,比较基础.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
17.一个几何体的三视图如图所示,则三视图表示的几何体的体积最大为( )
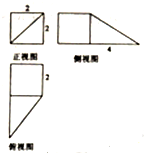

| A. | $\frac{40}{3}$ | B. | 40 | C. | $\frac{20}{3}$ | D. | 20 |
16.已知13+23+33+…+n3=$\frac{{{n^2}{{(an+b)}^2}}}{4}$对一切n∈N+都成立,那么a,b的可能值为( )
| A. | a=b=1 | B. | a=1,b=2 | C. | a=2,b=1 | D. | 不存在这样的a,b |
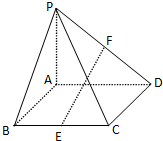 如图,在四棱锥P-ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,点E,F分别为BC、PD的中点,若PA=AD=4,AB=2.
如图,在四棱锥P-ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,点E,F分别为BC、PD的中点,若PA=AD=4,AB=2.