题目内容

19．在古希腊，毕达哥拉斯学派把1，3，6，10，15，…这些数叫做三角形数，因为这些数目的石子可以排成一个正三角形（如图），则第10个三角形数是（　　）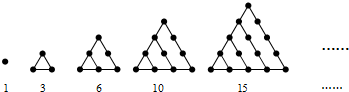
A．35B．36C．45D．55

分析 设第n个三角形数即第n个图中有an个点；观察图形可得，第二个图中点的个数比第一个图中点的个数多2，即a2-a1=2，第三个图中点的个数比第二个图中点的个数多3，即a3-a2=3，依此类推，可得第n个图中点的个数比第n-1个图中点的个数多n，即an-an-1=n，将得到的式子，相加可得答案．

解答 解：设第n个三角形数即第n个图中有an个点；
由图可得：
第二个图中点的个数比第一个图中点的个数多2，即a2-a1=2，
第三个图中点的个数比第二个图中点的个数多3，即a3-a2=3，
…
第n个图中点的个数比第n-1个图中点的个数多n，即an-an-1=n，
则an=1+2+3+4+…+n=$\frac{n（n+1）}{2}$，
n=10时，a10=55．
故选：D．

点评 本题主要考查了归纳推理，属于基础题．解题的关键在于观察、发现图形中点的个数的变化规律．

练习册系列答案
相关题目
9．已知函数f（x）=ex-m+ln$\frac{3}{x}$．
（Ⅰ）设x=1是函数f（x）的极值点，求m的值并讨论f（x）的单调性；
（Ⅱ）当m≤2时，证明：f（x）＞ln3．
10．已知函数f（x）=（2ax-lnx）x有两个极值点，则实数a的取值范围是（　　）
A．（0，$\frac{1}{4}$）B．（0，$\frac{1}{2}$）C．（0，1）D．（0，+∞）
7．抛物线y2=16x的焦点到准线的距离是（　　）
A．1B．2C．4D．8
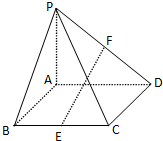14．如图，在四棱锥P-ABCD中，底面ABCD为矩形，侧棱PA⊥底面ABCD，点E，F分别为BC、PD的中点，若PA=AD=4，AB=2．
（1）求证：EF∥平面PAB．
（2）求直线EF与平面PCD所成的角．
4．若将一个45°的直角三角板的一直角边放在一桌面上，另一直角边与桌面所成角为45°，则此时该三角板的斜边与桌面所成的角等于30°．
11．记Sk=1k+2k+3k+…+nk，当k=1，2，3…时，观察下列等式：
S1=$\frac{1}{2}{n}^{2}+\frac{1}{2}n$，S2=$\frac{1}{3}{n}^{3}+\frac{1}{2}{n}^{2}+\frac{1}{6}n$，S3=$\frac{1}{4}{n}^{4}+\frac{1}{2}{n}^{3}+\frac{1}{4}{n}^{2}$，
S${\;}_{4}=\frac{1}{5}{n}^{5}+\frac{1}{2}{n}^{4}+\frac{1}{3}{n}^{3}-\frac{1}{30}n$，S5=$\frac{1}{6}{n}^{6}+A{n}^{5}+B{n}^{4}-\frac{1}{12}{n}^{2}$，…，
可以推测A-B=$\frac{1}{12}$．
8．已知函数f（x）=a+bcosx+csinx的图象经过点A（0，1）及$B（\frac{π}{2}，1）$
（1）已知b＞0，求f（x）的单调递减区间；
（2）已知$x∈（0，\frac{π}{2}）$时，|f（x）|≤2恒成立，求实数a的取值范围；
（3）当a取上述范围内的最大整数值时，若有实数m，n，φ，使得mf（x）+nf（x-φ）=1对于x∈R恒成立，求m，n，φ的值．
9．已知实数m，n满足2m-n=3．
（1）若|m|+|n+3|≥9，求实数m的取值范围；
（2）求$|{\frac{5}{3}m-\frac{1}{3}n}|+|{\frac{1}{3}m-\frac{2}{3}n}$|的最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网