题目内容
4.歌德巴赫(Goldbach.C.德.1690-1764)曾研究过“所有形如$\frac{1}{{{{(n+1)}^{m+1}}}}$(m,n为正整数)的分数之和”问题.为了便于表述,引入记号:$\sum_{n=1}^∞{\sum_{m=1}^∞{\frac{1}{{{{(n+1)}^{m+1}}}}}}$=$(\frac{1}{2^2}+\frac{1}{2^3}+\frac{1}{2^4}+…)+(\frac{1}{3^2}+\frac{1}{3^3}+\frac{1}{3^4}+…)+…+(\frac{1}{{{{(n+1)}^2}}}+\frac{1}{{{{(n+1)}^3}}}+\frac{1}{{{{(n+1)}^4}}}+…)+…$写出你对此问题的研究结论:$\sum_{n=1}^∞{\sum_{m=1}^∞{\frac{1}{{{{(n+1)}^{m+1}}}}=1}}$(用数学符号表示).
分析 分别求出$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+$\frac{1}{{2}^{4}}$+…,$\frac{1}{{3}^{2}}$+$\frac{1}{{3}^{3}}$+$\frac{1}{{3}^{4}}$+…,$\frac{1}{{(n+)}^{2}}$+$\frac{1}{{(n+1)}^{3}}$+$\frac{1}{{(n+1)}^{4}}$+…的极限,再代入∑n-1φ∑m-1φ$\frac{1}{{(n+1)}^{m+1}}$中,通过裂项法求得答案.
解答 解:$\sum_{n=1}^∞{\sum_{m=1}^∞{\frac{1}{{{{(n+1)}^{m+1}}}}}}$=$(\frac{1}{2^2}+\frac{1}{2^3}+\frac{1}{2^4}+…)+(\frac{1}{3^2}+\frac{1}{3^3}+\frac{1}{3^4}+…)+…+(\frac{1}{{{{(n+1)}^2}}}+\frac{1}{{{{(n+1)}^3}}}+\frac{1}{{{{(n+1)}^4}}}+…)+…$
=$\frac{\frac{1}{{2}^{2}}}{1-\frac{1}{2}}$+$\frac{\frac{1}{{3}^{2}}}{1-\frac{1}{3}}$+…+$\frac{\frac{1}{{(n+1)}^{2}}}{1-\frac{1}{n+1}}$
=$\frac{1}{2}$+$\frac{1}{2}$×$\frac{1}{3}$+$\frac{1}{3}$×$\frac{1}{4}$+…+$\frac{1}{n}$×$\frac{1}{n+1}$
=(1-$\frac{1}{2}$)+($\frac{1}{2}$-$\frac{1}{3}$)+($\frac{1}{3}$-$\frac{1}{4}$)+…+($\frac{1}{n}$-$\frac{1}{n+1}$)
=1-$\frac{1}{n+1}$,
当n→+∞时,$\sum_{n=1}^∞{\sum_{m=1}^∞{\frac{1}{{{{(n+1)}^{m+1}}}}}}$=1.
故答案为:$\sum_{n=1}^∞{\sum_{m=1}^∞{\frac{1}{{{{(n+1)}^{m+1}}}}}}$=1.
点评 本题主要考查了用裂项法求和的应用问题,是综合性问题.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
| A. | -7 | B. | -8 | C. | 3 | D. | 4 |
| A. | 空间中过直线外一点有且仅有一条直线与该直线垂直 | |
| B. | 仅存在一个实数b2,使得-9,b1,b2,b3,-1成等比数列 | |
| C. | 存在实数a,b满足a+b=2,使得3a+3b的最小值是6 | |
| D. | ?a∈(-4,0],ax2+ax-1<0恒成立 |
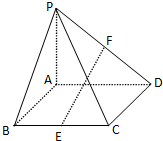 如图,在四棱锥P-ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,点E,F分别为BC、PD的中点,若PA=AD=4,AB=2.
如图,在四棱锥P-ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,点E,F分别为BC、PD的中点,若PA=AD=4,AB=2.