题目内容
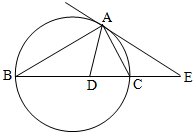 如图,△ABC的外接圆的切线AE与BC的延长线交于点E,∠BAC的平分线与BC交于点D.
如图,△ABC的外接圆的切线AE与BC的延长线交于点E,∠BAC的平分线与BC交于点D.(1)求证:ED2=EC•EB
(2)若BC是△ABC的外接圆的直径,且BC=2,CE=1.求AC长.
考点:与圆有关的比例线段
专题:选作题,立体几何
分析:(1)由弦切角定理,结合三角形的外角证出∠ADE=∠DAE,从而EA=ED.再由切割线定理,得EA2=EC•EB,结合EA=ED,即可证出ED2=EC•EB;
(2)利用△EAC∽△EBA,可得
=
=
,代入数据,即可得出结论.
(2)利用△EAC∽△EBA,可得
| EA |
| EB |
| AC |
| BA |
| EC |
| EA |
解答:
(1)证明:∵AE是圆的切线,∴∠ABC=∠CAE.
∵AD是∠BAC的平分线,∴∠BAD=∠CAD,
从而∠ABC+∠BAD=∠CAE+∠CAD.
∵∠ADE=∠ABC+∠BAD,∠DAE=∠CAD+∠CAE,
∴∠ADE=∠DAE,得EA=ED.
∵AE是圆的切线,∴由切割线定理,得EA2=EC•EB.
结合EA=ED,得ED2=EC•EB;
(2)解:∵AE是圆的切线,∴∠ABC=∠CAE,
∵∠E=∠E,
∴△EAC∽△EBA,
∴
=
=
,
∵BC=2,CE=1,
∴EA=
,
=
,
∵BC是△ABC的外接圆的直径,且BC=2,
∴AC=1.
∵AD是∠BAC的平分线,∴∠BAD=∠CAD,
从而∠ABC+∠BAD=∠CAE+∠CAD.
∵∠ADE=∠ABC+∠BAD,∠DAE=∠CAD+∠CAE,
∴∠ADE=∠DAE,得EA=ED.
∵AE是圆的切线,∴由切割线定理,得EA2=EC•EB.
结合EA=ED,得ED2=EC•EB;
(2)解:∵AE是圆的切线,∴∠ABC=∠CAE,
∵∠E=∠E,
∴△EAC∽△EBA,
∴
| EA |
| EB |
| AC |
| BA |
| EC |
| EA |
∵BC=2,CE=1,
∴EA=
| 3 |
| AC |
| BA |
| 1 | ||
|
∵BC是△ABC的外接圆的直径,且BC=2,
∴AC=1.
点评:本题主要考查三角形与圆的一些基础知识,如三角形的外接圆、角平分线,圆的切线性质、圆幂定理等.本题属基础题.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
用反证法证明命题:若p则q.其第一步是反设命题的结论不成立,这个正确的反设是( )
| A、若p,则¬q | B、若¬p,则q |
| C、¬p | D、¬q |
已知正方体ABCD-A1B1C1D1,平面BB1C1C内到直线AA1和直线BC距离相等的点的轨迹是( )
| A、圆 | B、椭圆 | C、双曲线 | D、抛物线 |
下列说法中正确的是( )
A、
| ||||||||
B、若
| ||||||||
C、若
| ||||||||
D、若
|
以下对象的全体不能构成集合的个数是( )
(1)高一(1)班的高个子同学;
(2)所有的数学难题;
(3)北京市中考分数580以上的同学;
(4)中国古代四大发明;
(5)我国的大河流;
(6)大于3的偶数.
(1)高一(1)班的高个子同学;
(2)所有的数学难题;
(3)北京市中考分数580以上的同学;
(4)中国古代四大发明;
(5)我国的大河流;
(6)大于3的偶数.
| A、2 | B、3 | C、4 | D、6 |
若F1,F2是椭圆
+
=1的两个焦点,A、B是过焦点F1的弦,则△ABF2的周长为( )
| x2 |
| 9 |
| y2 |
| 4 |
| A、6 | B、4 | C、12 | D、8 |