题目内容
在平面直角坐标系中,动点P到x轴的距离的平方恰比点P的横纵坐标的乘积小1.记动点P的轨迹为C,下列对于曲线C的描述正确的是
①曲线C关于原点对称;
②曲线C关于直线y=x对称;
③当变量|y|逐渐增大时,曲线C无限接近直线y=x;
④当变量|y|逐渐减小时,曲线C与x轴无限接近.
①曲线C关于原点对称;
②曲线C关于直线y=x对称;
③当变量|y|逐渐增大时,曲线C无限接近直线y=x;
④当变量|y|逐渐减小时,曲线C与x轴无限接近.
考点:轨迹方程
专题:圆锥曲线的定义、性质与方程
分析:设P(x,y),由题意可得:y2=xy-1,可得曲线C.
①把(-x,-y)代入曲线C得到y2=xy-1,曲线方程不变,即可得出对称性;
②把点(y,x)代入曲线C:得到曲线x2=xy-1,即可判断出曲线C关于直线y=x不对称;
③把曲线C的方程变为:
-
=1,当变量|y|逐渐增大时,
→0,
→1,可得曲线C无限接近直线y=x;
④曲线C的方程变为x=y+
,当变量|y|逐渐减小时,x→∞,可得曲线C与x轴无限接近.
①把(-x,-y)代入曲线C得到y2=xy-1,曲线方程不变,即可得出对称性;
②把点(y,x)代入曲线C:得到曲线x2=xy-1,即可判断出曲线C关于直线y=x不对称;
③把曲线C的方程变为:
| x |
| y |
| 1 |
| y2 |
| 1 |
| y2 |
| x |
| y |
④曲线C的方程变为x=y+
| 1 |
| y |
解答:
解:设P(x,y),由题意可得:y2=xy-1,可得曲线C.
①把(-x,-y)代入曲线C得到y2=xy-1,曲线方程不变,因此曲线C关于原点对称,正确;
②把点(y,x)代入曲线C:得到曲线x2=xy-1,可得曲线C关于直线y=x不对称,不正确;
③把曲线C的方程变为:
-
=1,当变量|y|逐渐增大时,
→0,
→1,因此曲线C无限接近直线y=x,正确;
④曲线C的方程变为x=y+
,当变量|y|逐渐减小时,x→∞,因此曲线C与x轴无限接近,正确.
综上可得:对于曲线C的描述正确的是①③④.
故答案为:①③④.
①把(-x,-y)代入曲线C得到y2=xy-1,曲线方程不变,因此曲线C关于原点对称,正确;
②把点(y,x)代入曲线C:得到曲线x2=xy-1,可得曲线C关于直线y=x不对称,不正确;
③把曲线C的方程变为:
| x |
| y |
| 1 |
| y2 |
| 1 |
| y2 |
| x |
| y |
④曲线C的方程变为x=y+
| 1 |
| y |
综上可得:对于曲线C的描述正确的是①③④.
故答案为:①③④.
点评:本题考查了曲线的轨迹及其性质,考查了推理能力,属于中档题.

练习册系列答案
相关题目
已知正方体ABCD-A1B1C1D1,平面BB1C1C内到直线AA1和直线BC距离相等的点的轨迹是( )
| A、圆 | B、椭圆 | C、双曲线 | D、抛物线 |
以下对象的全体不能构成集合的个数是( )
(1)高一(1)班的高个子同学;
(2)所有的数学难题;
(3)北京市中考分数580以上的同学;
(4)中国古代四大发明;
(5)我国的大河流;
(6)大于3的偶数.
(1)高一(1)班的高个子同学;
(2)所有的数学难题;
(3)北京市中考分数580以上的同学;
(4)中国古代四大发明;
(5)我国的大河流;
(6)大于3的偶数.
| A、2 | B、3 | C、4 | D、6 |
若F1,F2是椭圆
+
=1的两个焦点,A、B是过焦点F1的弦,则△ABF2的周长为( )
| x2 |
| 9 |
| y2 |
| 4 |
| A、6 | B、4 | C、12 | D、8 |
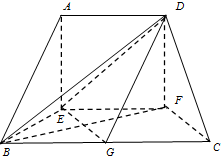 已知在如图的多面体中,AE⊥底面BEFC,AD∥EF∥BC,CF=BE=AD=EF=
已知在如图的多面体中,AE⊥底面BEFC,AD∥EF∥BC,CF=BE=AD=EF=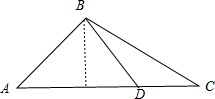 如图,一个三角形的绿地ABC,AB边的长为7m,由C点看AB的张角为45°,在AC边上一点D处看AB的张角为60°,且AD=2DC,试求这块绿地的面积.
如图,一个三角形的绿地ABC,AB边的长为7m,由C点看AB的张角为45°,在AC边上一点D处看AB的张角为60°,且AD=2DC,试求这块绿地的面积.