题目内容
已知lg(a-1)+lg(b-2)=lg2,则a+b的范围是 .
考点:对数的运算性质
专题:函数的性质及应用
分析:由题意可得a-1>0且b-2>0,(a-1)(b-2)=2,由基本不等式可得2=(a-1)(b-2)≤(
)2,解关于a+b的不等式可得.
| a-1+b-2 |
| 2 |
解答:
解:∵lg(a-1)+lg(b-2)=lg2,
∴a-1>0且b-2>0,(a-1)(b-2)=2,
∴2=(a-1)(b-2)≤(
)2=
,
∴(a+b-3)2≥8,解得a+b-3≥2
,或a+b-3≤-2
(舍去),
∴a+b≥3+2
,当期仅当(a-1)=(b-2)即a=b-1时取等号,
故答案为:[3+2
,+∞)
∴a-1>0且b-2>0,(a-1)(b-2)=2,
∴2=(a-1)(b-2)≤(
| a-1+b-2 |
| 2 |
| (a+b-3)2 |
| 4 |
∴(a+b-3)2≥8,解得a+b-3≥2
| 2 |
| 2 |
∴a+b≥3+2
| 2 |
故答案为:[3+2
| 2 |
点评:本题考查对数的运算性质,涉及基本不等式的应用,属中档题.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
以下对象的全体不能构成集合的个数是( )
(1)高一(1)班的高个子同学;
(2)所有的数学难题;
(3)北京市中考分数580以上的同学;
(4)中国古代四大发明;
(5)我国的大河流;
(6)大于3的偶数.
(1)高一(1)班的高个子同学;
(2)所有的数学难题;
(3)北京市中考分数580以上的同学;
(4)中国古代四大发明;
(5)我国的大河流;
(6)大于3的偶数.
| A、2 | B、3 | C、4 | D、6 |
若F1,F2是椭圆
+
=1的两个焦点,A、B是过焦点F1的弦,则△ABF2的周长为( )
| x2 |
| 9 |
| y2 |
| 4 |
| A、6 | B、4 | C、12 | D、8 |
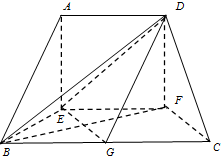 已知在如图的多面体中,AE⊥底面BEFC,AD∥EF∥BC,CF=BE=AD=EF=
已知在如图的多面体中,AE⊥底面BEFC,AD∥EF∥BC,CF=BE=AD=EF= 在正方体ABCD-A1B1C1D1中,E,F分别为DD1,BD的中点.求证:
在正方体ABCD-A1B1C1D1中,E,F分别为DD1,BD的中点.求证: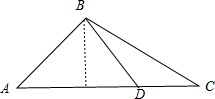 如图,一个三角形的绿地ABC,AB边的长为7m,由C点看AB的张角为45°,在AC边上一点D处看AB的张角为60°,且AD=2DC,试求这块绿地的面积.
如图,一个三角形的绿地ABC,AB边的长为7m,由C点看AB的张角为45°,在AC边上一点D处看AB的张角为60°,且AD=2DC,试求这块绿地的面积.