题目内容
3.在平面直角坐标系中,已知椭圆两焦点坐标为F1(-2$\sqrt{2}$,0),F2(2$\sqrt{2}$,0),椭圆C上的点到右焦点距离最小值为3-2$\sqrt{2}$.(1)求椭圆C的方程;
(2)设斜率为-2的直线交曲线C于E、F两点,求线段EF的中点N的轨迹方程;
(3)设经过点F1(-2$\sqrt{2}$,0)的直线与曲线C相交所得的弦为线段PQ,求△PQO的面积的最大值(O是坐标原点).
分析 (1)由c=2$\sqrt{2}$,a-c=3-2$\sqrt{2}$.a=3,b2=a2-c2=1即可求得椭圆方程;
(2)方法一:设直线方程为y=-2x+t,代入椭圆方程,利用韦达定理及中点坐标公式,消去t,即可求得轨迹方程,代入椭圆方程,即可求得x的取值范围;方法二:利用设而不求法,将E和F坐标代入椭圆方程,作差,根据中点坐标公式,即可求得即可求得轨迹方程,代入椭圆方程,即可求得x的取值范围;
(3)设直线方程,代入椭圆方程,利用韦达定理,弦长公式,根据函数的单调性即可求得△PQO的面积的最大值.
解答 解:(1)椭圆的焦点为${F_1}(-2\sqrt{2},0),{F_2}(2\sqrt{2},0)$,c=2$\sqrt{2}$,
由a-c=3-2$\sqrt{2}$.a=3,则b2=a2-c2=1
故曲线C的方程为$\frac{x^2}{9}+{y^2}=1$.
(2)方法1:设A(x1,y1),B(x2,y2),N(x,y),设直线方程为y=-2x+t,
$\left\{\begin{array}{l}{y=-2x+t}\\{\frac{{x}^{2}}{9}+{y}^{2}=1}\end{array}\right.$,$\frac{37}{9}{x}^{2}$-4tx+t2-1=0,$2x={x_1}+{x_2}=\frac{36}{37}t\;,\;2y={y_1}+{y_2}=-2({x_1}+{x_2})+2t=\frac{2}{37}t$,
∴x-18y=0,
$\left\{\begin{array}{l}{x-18y=0}\\{\frac{{x}^{2}}{9}+{y}^{2}=1}\end{array}\right.$,则x2=±$\frac{18\sqrt{37}}{37}$,则-$\frac{18\sqrt{37}}{37}$<x<$\frac{18\sqrt{37}}{37}$,
∴线段EF的中点N的轨迹方程是:x-18y=0,-$\frac{18\sqrt{37}}{37}$<x<$\frac{18\sqrt{37}}{37}$,
方法2:设A(x1,y1),B(x2,y2),N(x,y),则x1+x2=2x,y1+y2=2y.
∵A、B在曲线C上,
∴$x_1^2+9y_1^2=9$,$x_2^2+9y_2^2=9$.
将以上两式相减得:(x1-x2)(x1+x2)+9(y1-y2)(y2+y2)=0,即$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=-$\frac{{x}_{1}+{x}_{2}}{9({y}_{1}+{y}_{2})}$,
则-2=-$\frac{x}{9y}$,
∴线段EF的中点N的轨迹方程:x-18y=0,-$\frac{18\sqrt{37}}{37}$<x<$\frac{18\sqrt{37}}{37}$;
(3)设直线PQ的方程是:my=x+2$\sqrt{2}$,x=my-2$\sqrt{2}$,
代入$\frac{x^2}{9}+{y^2}=1$得$({m^2}+9){y^2}-4\sqrt{2}my-1=0$.
设P(x1,y1),Q(x2,y2),${y_1}+{y_2}=\frac{{4\sqrt{2}m}}{{{m^2}+9}}$,${y_1}•{y_2}=\frac{-1}{{{m^2}+9}}$,
则$|{y_1}-{y_2}|\;=6\sqrt{\frac{{{m^2}+1}}{{{{({m^2}+9)}^2}}}}$,
令t=m2+9≥9,$|{y_1}-{y_2}|\;=6\sqrt{\frac{t-8}{t^2}}=6\sqrt{-\frac{8}{t^2}+\frac{1}{t}}=6\sqrt{-8{{(\frac{1}{t}-\frac{1}{16})}^2}+\frac{8}{{{{16}^2}}}}$,
当t=16,即$m=±\sqrt{7}$时,
∴${({S_{△OPQ}})_{max}}=\frac{1}{2}|OF|•|{y_1}-{y_2}|\;=\frac{3}{2}$,
△PQO的面积的最大值为$\frac{3}{2}$.
点评 本题考查椭圆的标准方程,直线与椭圆的位置关系,考查韦达定理,弦长公式,轨迹方程的求法,考查函数单调性与椭圆的综合应用,考查计算能力,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | c>b>a | B. | a>b>c | C. | a>c>b | D. | b>a>c |
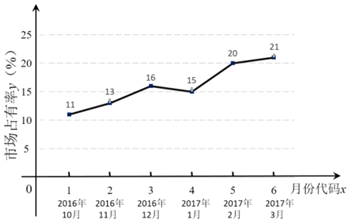
(Ⅰ)由折线图可以看出,可用线性回归模型拟合月度市场占有率y与月份代码x之间的关系.求y关于x的线性回归方程,并预测M公司2017年4月份的市场占有率;
(Ⅱ)为进一步扩大市场,公司拟再采购一批单车.现有采购成本分别为1000元/辆和1200元/辆的A、B两款车型可供选择,按规定每辆单车最多使用4年,但由于多种原因(如骑行频率等)会导致车辆报废年限各不相同.考虑到公司运营的经济效益,该公司决定先对两款车型的单车各100辆进行科学模拟测试,得到两款单车使用寿命频数表如下:
报废年限 车型 | 1年 | 2年 | 3年 | 4年 | 总计 |
| A | 20 | 35 | 35 | 10 | 100 |
| B | 10 | 30 | 40 | 20 | 100 |
参考数据:,$\sum_{i=1}^6{({x_i}-\overline x)({y_i}}-\overline y)=35$,$\sum_{i=1}^6{{{({x_i}-\overline x)}^2}}$=17.5.
参考公式:
回归直线方程为$\hat y=\hat bx+\hat a$其中$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}$=$\widehat{y}$-$\widehat{b}$$\overline{t}$.
 在直角坐标系xOy中,椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{2}}}{2}$,左、右焦点分别是F1,F2,P为椭圆C1上任意一点,|PF1|+|PF2|的最大值为4.
在直角坐标系xOy中,椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{2}}}{2}$,左、右焦点分别是F1,F2,P为椭圆C1上任意一点,|PF1|+|PF2|的最大值为4.