题目内容
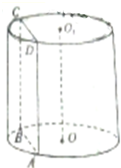 已知圆柱OO1的底面半径为2,高为4.
已知圆柱OO1的底面半径为2,高为4.(1)求从下底面出发环绕圆柱侧面一周到达上底面的最短路径长;
(2)若平行于轴OO1的截面ABCD将底面圆周截取四分之一,求截面面积;
(3)在(2)的条件下,设截面将圆柱分成的两部分中较小部分为Ⅰ,较大部分为Ⅱ,求
VⅠ:VⅡ(体积之比)
考点:棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:(1)根据侧面展开图的对角线即可是最短距离,(2)转化为VⅠ:VⅡ=SⅠ:SⅡ,利用圆的知识求解面积,即可得出体积之比.
解答:
解:
(1)根据侧面展开图得出:
从下底面出发环绕圆柱侧面一周到达上底面的最短路径长为
=4
,
(2)根据题意可得:△OAB为等腰直角三角形,OA=OB=2
∴AB=2
,
∴截面面积为:2
×4=8
.
(3)根据题意可得:
底面为4π,
SⅠ=
-
×22=π-2,
SⅡ=3π+2
VⅠ:VⅡ=SⅠ:SⅡ=
故:
=

(1)根据侧面展开图得出:
从下底面出发环绕圆柱侧面一周到达上底面的最短路径长为
| 42+(2π×2)2 |
| π2+1 |
(2)根据题意可得:△OAB为等腰直角三角形,OA=OB=2
∴AB=2
| 2 |
∴截面面积为:2
| 2 |
| 2 |
(3)根据题意可得:
底面为4π,
SⅠ=
| π×22 |
| 4 |
| 1 |
| 2 |
SⅡ=3π+2
VⅠ:VⅡ=SⅠ:SⅡ=
| π-2 |
| 3π+2 |
故:
| VⅠ |
| VⅡ |
| π-2 |
| 3π+2 |
点评:本题综合考查了空间几何体的性质,面积,体积公式,属于计算题,考虑好所求线段即可.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
在△ABC中,角A,B,C所对应的边分别为a,b,c,则“a≥b”是“sinA≥sinB”的( )
| A、充分必要条件 |
| B、充分而非必要条件 |
| C、必要非充分条件 |
| D、非充分非必要条件 |
函数f(x)=
的定义域为( )
| lg(x-1) | ||
|
| A、(-∞,-2)∪(1,+∞) |
| B、(-2,1) |
| C、(-∞,-1)∪(2,+∞) |
| D、(1,2) |
 如图,已知点P(m,n)(m,n>0)在椭圆
如图,已知点P(m,n)(m,n>0)在椭圆| x2 |
| 16 |
| y2 |
| 9 |
| A、24 | B、18 | C、12 | D、6 |