题目内容
下列哪一组函数相等( )
A、f(x)=x与g(x)=
| |||
B、f(x)=x2与g(x)=(
| |||
C、f(x)=|x|与g(x)=(
| |||
D、f(x)=x2与g(x)=
|
考点:判断两个函数是否为同一函数
专题:计算题,函数的性质及应用
分析:判断函数是否相等要看两个方面,对应关系与定义域.
解答:
解:f(x)=x的定义域为R,g(x)=
的定义域为{x|x≠0},故不相等;
f(x)=x2的定义域为R,g(x)=(
)4的定义域为[0,+∞),故不相等;
f(x)=|x|的定义域为R,g(x)=(
)2的定义域为[0,+∞),故不相等;
f(x)=x2与g(x)=
的定义域及对应关系都相同,故相等;
故选D.
| x2 |
| x |
f(x)=x2的定义域为R,g(x)=(
| x |
f(x)=|x|的定义域为R,g(x)=(
| x |
f(x)=x2与g(x)=
| 3 | x6 |
故选D.
点评:本题考查了函数相等的判断,只需对定义域与对应关系两者都判断即可.

练习册系列答案
相关题目
如果f(a+b)=f(a)•f(b)且f(1)=2,则
+
+
+…+
=( )
| f(2) |
| f(1) |
| f(4) |
| f(3) |
| f(6) |
| f(5) |
| f(2014) |
| f(2013) |
| A、2012 | B、1007 |
| C、2014 | D、2013 |
若A∈α,B∈α,A∈l,B∈l,P∈l,则( )
| A、P?α | B、P∉α |
| C、l?α | D、P∈α |
函数f(x)=log2(x+4)-3x的零点有( )
| A、0 | B、1 | C、2 | D、3 |
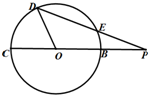 如图,割线PBC经过圆心O,OB=PB=1,又PED交圆O于E,D,且DE=
如图,割线PBC经过圆心O,OB=PB=1,又PED交圆O于E,D,且DE=