题目内容
已知f(x)是定义在R上的奇函数,且对任意实数x∈R均有f(x-1)=f(x+1),当x∈[0,1)时,f(x)=2x-1,则f(log
6)= .
| 1 |
| 2 |
考点:函数的周期性,对数函数图象与性质的综合应用
专题:函数的性质及应用
分析:由已知中对任意实数x∈R均有f(x-1)=f(x+1),可得:函数f(x)是周期为2的周期函数,又由log
6∈(-3,-2),可得:log
6+2∈(-1,0),即-log
6-2∈(0,1),故f(log
6)=f(log
6+2)=-f(-log
6-2),利用对数的运算性质化简可得答案.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:∵对任意实数x∈R均有f(x-1)=f(x+1),
故f(x+2)=f(x),即函数f(x)是周期为2的周期函数,
又由f(x)是定义在R上的奇函数,
∴f(-x)=-f(x),
∵log
6∈(-3,-2),
∴log
6+2∈(-1,0),
∴-log
6-2∈(0,1),
∴f(log
6)=f(log
6+2)=-f(-log
6-2)=-[2(-log
6-2)-1]=2log
6+5=3-2log23,
故答案为:3-2log23
故f(x+2)=f(x),即函数f(x)是周期为2的周期函数,
又由f(x)是定义在R上的奇函数,
∴f(-x)=-f(x),
∵log
| 1 |
| 2 |
∴log
| 1 |
| 2 |
∴-log
| 1 |
| 2 |
∴f(log
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:3-2log23
点评:本题考查的知识点是对数的运算性质,函数的奇偶性,函数的周期性,是函数图象和性质的综合应用,难度中档.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
函数f(x)=log2(x+4)-3x的零点有( )
| A、0 | B、1 | C、2 | D、3 |
已知双曲线C1:
-
=1(a>0,b>0)与抛物线C2:y2=2px(p>0)有相同焦点,若双曲线C1与抛物线C2的一个公共点为P,且点P到抛物线的准线的距离为p,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
B、
| ||
| C、2 | ||
D、2+
|
设f(n)=2+24+27+210+…+23n+10(n∈N),则f(n)等于( )
A、
| ||
B、
| ||
C、
| ||
D、
|
直线平分圆x2+y2-2x-4y+1=0的周长,则此直线的方程可能是( )
| A、x-y+1=0 |
| B、x+y+3=0 |
| C、x+y-1=0 |
| D、x-y+3=0 |
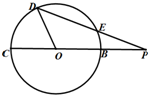 如图,割线PBC经过圆心O,OB=PB=1,又PED交圆O于E,D,且DE=
如图,割线PBC经过圆心O,OB=PB=1,又PED交圆O于E,D,且DE=