题目内容
如图所示椭圆中,P为椭圆上一点,F为其一个焦点,PF为直径的圆与长轴为直径的圆的关系为 .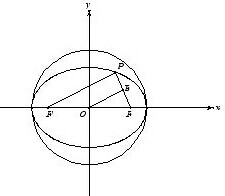

考点:椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
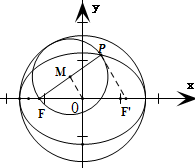
分析:设F、F'分别是椭圆的左右焦点,作出以PF为直径的圆和以长轴为直径的圆x2+y2=a2,如图所示.设PF的中点为M,连结PF',利用三角形中位线定理与椭圆的定义,证出|OM|=
|PF'|=a-
|PF|,得到两圆的圆心距等于它们半径之差,从而得到两圆的位置关系是相内切.
| 1 |
| 2 |
| 1 |
| 2 |
解答:
 解:设椭圆的方程为
解:设椭圆的方程为
+
=1(a>b>0),F、F'分别是椭圆的左右焦点,
作出以线段PF为直径的圆和以长轴为直径的圆x2+y2=a2,如图所示.
设PF中点为M,连结PF',
∴OM是△PFF'的中位线,可得|OM|=
|PF'|,即两圆的圆心距为
|PF'|
根据椭圆定义,可得|PF|+|PF'|=2a,
∴圆心距|OM|=
|PF'|=
(2a-|PF|)=a-
|PF|,
即两圆的圆心距等于它们半径之差,
因此,以PF为直径的圆与以长半轴为直径的圆x2+y2=a2相内切.
故答案为:内切.
 解:设椭圆的方程为
解:设椭圆的方程为| x2 |
| a2 |
| y2 |
| b2 |
作出以线段PF为直径的圆和以长轴为直径的圆x2+y2=a2,如图所示.
设PF中点为M,连结PF',
∴OM是△PFF'的中位线,可得|OM|=
| 1 |
| 2 |
| 1 |
| 2 |
根据椭圆定义,可得|PF|+|PF'|=2a,
∴圆心距|OM|=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即两圆的圆心距等于它们半径之差,
因此,以PF为直径的圆与以长半轴为直径的圆x2+y2=a2相内切.
故答案为:内切.
点评:本题给出椭圆以一条焦半径为直径的圆和以长轴为直径的圆,求两圆的位置关系.着重考查了圆与圆的位置关系及其证明、椭圆的定义与简单几何性质等知识,属于中档题.

练习册系列答案
相关题目
△ABC中,M是BC边的中点,则向量
等于( )
| AM |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
