题目内容
已知函数f(x)=
sin
cos
+sin2
(ω>0),0<φ<
).其图象的两个相邻对称中心的距离为
,且过点(
,
),则φ .
| 3 |
| ωx+φ |
| 2 |
| ωx+φ |
| 2 |
| ωx+φ |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 6 |
| 3 |
| 2 |
考点:三角函数中的恒等变换应用
专题:三角函数的图像与性质
分析:先利用二倍角公式和两角和公式对函数解析式化简,进而根据对称中心的距离求得周期,则ω可求,最后根据点(
,
),求得φ.
| π |
| 6 |
| 3 |
| 2 |
解答:
解:f(x)=
sin
cos
+sin2
=
sin(ωx+φ)-
+
=sin(ωx+φ-
)+
,
∵图象的两个相邻对称中心的距离为
,
∴函数的周期T=π,
∴ω=
=2,
∴f(x)=sin(2x+φ-
)+
,
f(
)=sin(
+φ-
)+
=
,
∴sin(φ+
)=1,
∴φ+
=2kπ+
,
∴φ=2kπ+
,k∈Z,
∵0<φ<
,
∴φ=
.
| 3 |
| ωx+φ |
| 2 |
| ωx+φ |
| 2 |
| ωx+φ |
| 2 |
| ||
| 2 |
| cos(ωx+φ) |
| 2 |
| 1 |
| 2 |
| π |
| 6 |
| 1 |
| 2 |
∵图象的两个相邻对称中心的距离为
| π |
| 2 |
∴函数的周期T=π,
∴ω=
| 2π |
| T |
∴f(x)=sin(2x+φ-
| π |
| 6 |
| 1 |
| 2 |
f(
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
| 1 |
| 2 |
| 3 |
| 2 |
∴sin(φ+
| π |
| 6 |
∴φ+
| π |
| 6 |
| π |
| 2 |
∴φ=2kπ+
| π |
| 3 |
∵0<φ<
| π |
| 2 |
∴φ=
| π |
| 3 |
点评:本题主要考查了三角函数图象与性质,三角函数恒等变换的应用.考查了学生对三角函数性质和图象的熟练记忆.

练习册系列答案
相关题目
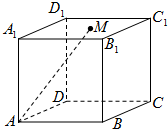
如图,ABCD-A1B1C1D1是正方体,在底面A1B1C1D1上任取一点M,则∠MAA1≤
的概率P=( )
| π |
| 6 |

A、
| ||
B、
| ||
C、
| ||
D、
|
已知集合S={x||x-1|≤2,x∈R},T={x|
≥0,x∈Z},则S∩T=( )
| 5 |
| x+1 |
| A、{x|0<x<3,x∈Z} |
| B、{x|0≤x≤3,x∈Z} |
| C、{x|-1≤x≤3,x∈Z} |
| D、{x|-1<x<3,x∈Z} |