题目内容
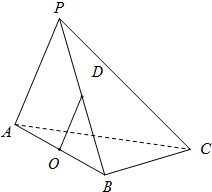 在三棱锥P-ABC中△PAC,△PBC是边长为
在三棱锥P-ABC中△PAC,△PBC是边长为| 2 |
(1)求证:OD∥平面PAC;
(2)求证PAB⊥平面ABC;
(3)求三棱锥P-ABC的体积.
考点:棱柱、棱锥、棱台的体积,平面与平面垂直的判定
专题:空间位置关系与距离
分析:(1)欲证OD∥平面PAC,根据直线与平面平行的判定定理可知只需证OD与平面PAC内一直线平行,而OD∥PA,PA?平面PAC,OD?平面PAC,满足定理条件;
(2)欲证平面PAB⊥平面ABC,根据面面垂直的判定定理可知在平面PAB内一直线与平面ABC垂直,而根据题意可得PO⊥平面ABC;
(3)根据OP垂直平面ABC得到OP为三棱锥P-ABC的高,根据三棱锥的体积公式可求出三棱锥P-ABC的体积.
(2)欲证平面PAB⊥平面ABC,根据面面垂直的判定定理可知在平面PAB内一直线与平面ABC垂直,而根据题意可得PO⊥平面ABC;
(3)根据OP垂直平面ABC得到OP为三棱锥P-ABC的高,根据三棱锥的体积公式可求出三棱锥P-ABC的体积.
解答:
 (1)证明:∵O,D分别为AB,PB的中点,
(1)证明:∵O,D分别为AB,PB的中点,
∴OD∥AP,
∵AP?平面PAC,OD?平面PAC,
∴OD∥平面PAC;
(2)证明:根据(1)连接OC,OP
∵AC=CB=
,O为AB中点,AB=2,
∴OC⊥AB,OC=1.
同理,PO⊥AB,PO=1.
又PC=
,
∴PC2=OC2+PO2=2,
∴∠POC=90°.
∴PO⊥OC.
∵PO⊥OC,PO⊥AB,AB∩OC=O,
∴PO⊥平面ABC.PO?平面PAB
∴平面PAB⊥平面ABC.
解:(3)由(2)可知OP垂直平面ABC,
∴OP为三棱锥P-ABC的高,且OP=1
∴VP-ABC=
×S△ABC•OP=
×2×
×1=
.
 (1)证明:∵O,D分别为AB,PB的中点,
(1)证明:∵O,D分别为AB,PB的中点,∴OD∥AP,
∵AP?平面PAC,OD?平面PAC,
∴OD∥平面PAC;
(2)证明:根据(1)连接OC,OP
∵AC=CB=
| 2 |
∴OC⊥AB,OC=1.
同理,PO⊥AB,PO=1.

又PC=
| 2 |
∴PC2=OC2+PO2=2,
∴∠POC=90°.
∴PO⊥OC.
∵PO⊥OC,PO⊥AB,AB∩OC=O,
∴PO⊥平面ABC.PO?平面PAB
∴平面PAB⊥平面ABC.
解:(3)由(2)可知OP垂直平面ABC,
∴OP为三棱锥P-ABC的高,且OP=1
∴VP-ABC=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
点评:本题主要考查直线与平面平行的判定,以及平面与平面垂直的判定和三棱锥的体积的计算,体积的求解在最近两年高考中频繁出现,值得重视.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
某工厂购买了某种设备,该设备正常使用使用n年的使用成本,含购设备在费维修费保养费以及使用设备所需的电费油费等费用的总费用为f(n)=
n2+12n+10(n∈N*,1≤n≤20),则年平均使用成本即
最低为( )
| 1 |
| 10 |
| f(n) |
| n |
| A、8 | B、14 | C、12 | D、20 |
已知函数f(x)=
,若f(x)≥ax恒成立,则a的取值范围是( )
|
A、(∞,
| ||||
B、[-
| ||||
C、[
| ||||
| D、[1,+∞) |
若
,
是夹角为
的单位向量,
=
-2
=
+
,则
•
=( )
| a |
| b |
| π |
| 3 |
| m |
| a |
| b, |
| n |
| a |
| b |
| m |
| n |
| A、1 | ||
B、-
| ||
C、
| ||
| D、-1 |
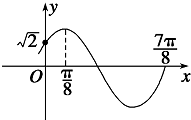 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<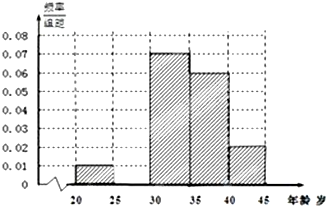 某市要对2000多名出租车司机的年龄进行调查,现从中随机抽出100名司机,已知抽到的司机年龄都在[20,45)岁之间,根据调查结果得出司机的年龄情况残缺的频率分布直方图如图所示.
某市要对2000多名出租车司机的年龄进行调查,现从中随机抽出100名司机,已知抽到的司机年龄都在[20,45)岁之间,根据调查结果得出司机的年龄情况残缺的频率分布直方图如图所示.