题目内容
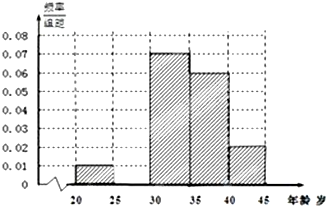 某市要对2000多名出租车司机的年龄进行调查,现从中随机抽出100名司机,已知抽到的司机年龄都在[20,45)岁之间,根据调查结果得出司机的年龄情况残缺的频率分布直方图如图所示.
某市要对2000多名出租车司机的年龄进行调查,现从中随机抽出100名司机,已知抽到的司机年龄都在[20,45)岁之间,根据调查结果得出司机的年龄情况残缺的频率分布直方图如图所示.(1)请你把上述的频率分布直方图补充完整;
(2)司机年龄位于[30,40)的有多少名?
(3)估计该市出租车司机年龄的中位数大约是多少?
考点:频率分布直方图,极差、方差与标准差
专题:概率与统计
分析:(1)计算年龄在[25,30)的概率,求出年龄在[25,30)的小矩形图的高即可;
(2)求出司机年龄位于[30,40)的频率与频数即可;
(3)求出数据的中位数即可.
(2)求出司机年龄位于[30,40)的频率与频数即可;
(3)求出数据的中位数即可.
解答:
解:(1)根据频率分布直方图得,年龄在[25,30)的概率是
1-(0.01+0.07+0.06+0.02)×5=0.2,
∴年龄在[25,30)的小矩形图的高是
=0.04,
把频率分布直方图补充完整即可;
(2)司机年龄位于[30,40)的频率是(0.07+0.06)×5=0.65,
∴对应的司机人数是100×0.65=65;
(3)∵0.01×5+0.2+=0.25<0.5,
0.01×5+0.2+0.07×5=0.6>0.5,
设x,令0.01×5+0.2+0.07×x=0.5,
解得x≈4,
∴估计该市出租车司机年龄的中位数大约是30+4=34.
1-(0.01+0.07+0.06+0.02)×5=0.2,
∴年龄在[25,30)的小矩形图的高是
| 0.2 |
| 5 |
把频率分布直方图补充完整即可;
(2)司机年龄位于[30,40)的频率是(0.07+0.06)×5=0.65,
∴对应的司机人数是100×0.65=65;
(3)∵0.01×5+0.2+=0.25<0.5,
0.01×5+0.2+0.07×5=0.6>0.5,
设x,令0.01×5+0.2+0.07×x=0.5,
解得x≈4,
∴估计该市出租车司机年龄的中位数大约是30+4=34.
点评:本题考查了频率分布直方图的应用问题,解题时应根据直方图进行简单的计算,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列函数中,在(0,+∞)既是增函数又是奇函数的是( )
| A、y=x+1 | ||
B、y=x+
| ||
C、y=x-
| ||
| D、y=x2+1 |
若实数x,y满足线性约束条件
,则z=2x+y的最大值为( )
|
| A、0 | B、4 | C、5 | D、7 |
 某选手参加演讲比赛的一次评委打分如茎叶图所示,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )
某选手参加演讲比赛的一次评委打分如茎叶图所示,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )| A、86.5,1.5 |
| B、86.5,1.2 |
| C、86,1.5 |
| D、86,1.2 |
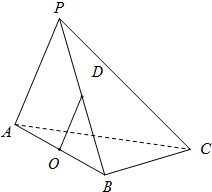 在三棱锥P-ABC中△PAC,△PBC是边长为
在三棱锥P-ABC中△PAC,△PBC是边长为 为了解我县中学生的体质状况,对天义地区部分中学生进行了身高、体重和肺活量的抽样调查.现随机抽取100名学生,测得其身高情况如下表所示.
为了解我县中学生的体质状况,对天义地区部分中学生进行了身高、体重和肺活量的抽样调查.现随机抽取100名学生,测得其身高情况如下表所示.