题目内容
已知tanα=-
,求
sin2α+
cos2α的值.
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 4 |
考点:三角函数的化简求值
专题:三角函数的求值
分析:利用平方关系式,代换所求表达式的分母,转化为正切函数的形式棉短绒求解即可.
解答:
解:tanα=-
,
则
sin2α+
cos2α=
=
=
=
.
故答案为:
.
| 1 |
| 2 |
则
| 2 |
| 3 |
| 1 |
| 4 |
| ||||
| sin2α+cos2α |
| ||||
| tan2α+1 |
| ||||||
|
| 1 |
| 3 |
故答案为:
| 1 |
| 3 |
点评:本题考查三角函数的化简求值同角三角函数的基本关系式的应用,考查计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知函数f(x)是偶函数,且x≥0时,f(x)=sin2x,则f(-
)=( )
| 13π |
| 6 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
集合A={x|x2-2x>0},集合B是函数y=lg(2-x)的定义域,则A∩B=( )
| A、(-∞,0) |
| B、(0,1) |
| C、(1,2) |
| D、(2,+∞) |
已知圆柱的侧面展开图是边长分别为2a,a的矩形,则该圆柱的体积为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知△ABC的周长为
+1,面积为
sinC且sinA+sinB=
sinC,则角C为( )
| 2 |
| 1 |
| 6 |
| 2 |
| A、30° | B、60° |
| C、45° | D、90° |
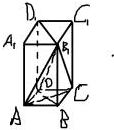 如图,在直棱柱ABCD-A1B1C1D1中,AA1=4,底面是边长为2的菱形,且∠BAD=60°.
如图,在直棱柱ABCD-A1B1C1D1中,AA1=4,底面是边长为2的菱形,且∠BAD=60°.