题目内容
已知x∈(0,3),则函数y=
+
的最小值为 .
| 1 |
| x |
| 4 |
| 3-x |
考点:基本不等式
专题:函数的性质及应用
分析:利用
+
≥
,当且仅当
=
时取等号,x,y,m,n都为正数.
| m2 |
| x |
| n2 |
| y |
| (m+n)2 |
| x+y |
| m |
| x |
| n |
| y |
解答:
解:∵x∈(0,3),
∴函数y=
+
≥
=3,当且仅当
=
,即x=1时取等号.
∴函数y=
+
的最小值为3.
故答案为:3.
∴函数y=
| 1 |
| x |
| 4 |
| 3-x |
| (1+2)2 |
| x+3-x |
| 1 |
| x |
| 2 |
| 3-x |
∴函数y=
| 1 |
| x |
| 4 |
| 3-x |
故答案为:3.
点评:本题考查了变形利用基本不等式的性质,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
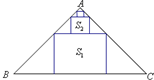 在等腰直角△ABC中,∠A=90°,BC=3,△ABC中排列着内接正方形,如图所示,若正方形的面积依次为S1,S2,…,Sn,…(从大到小),其中n∈N*,则
在等腰直角△ABC中,∠A=90°,BC=3,△ABC中排列着内接正方形,如图所示,若正方形的面积依次为S1,S2,…,Sn,…(从大到小),其中n∈N*,则| lim |
| n→∞ |
已知等差数列{an}的公差为2,若a1,a3,a4成等比数列,则a2的值为( )
| A、-4 | B、-10 | C、-8 | D、-6 |
已知集合A={y|y=-x2+3,x∈R},B={x|y=
},则A∩B=( )
| x+3 |
| A、{(0,3),(1,2)} |
| B、(-3,-3) |
| C、[-3,3] |
| D、{y|y≤3} |
若l、m、n是互不相同的空间直线,α、β是不重合的平面,则下列结论正确的是( )
| A、α∥β,l?α,n?β⇒l∥n |
| B、α∥β,l?α⇒l⊥β |
| C、l⊥n,m⊥n⇒l∥m |
| D、l⊥α,l∥β⇒α⊥β |
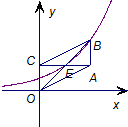 如图,面积为8的平行四边形OABC,对角线AC⊥OC,AC与BO交于点E,某指数函数y=ax(a>0,且a≠1)的图象经过点E,B,则a=( )
如图,面积为8的平行四边形OABC,对角线AC⊥OC,AC与BO交于点E,某指数函数y=ax(a>0,且a≠1)的图象经过点E,B,则a=( )