题目内容
不等式x2+ax+b≤0的解集是[-1，2]，则a+b的值是（ ）
| A、-3 | B、-1 | C、1 | D、3 |
考点：一元二次不等式的解法
专题：不等式的解法及应用
分析：不等式x2+ax+b≤0的解集是[-1，2]，可得-1，2是x2+ax+b=0的两个实数根，利用根与系数的关系即可得出．
解答：
解：∵不等式x2+ax+b≤0的解集是[-1，2]，
∴-1，2是x2+ax+b=0的两个实数根，
∴-1+2=-a，-1×2=b，
解得a=-1，b=-2．
∴a+b=-3．
故选：A．
∴-1，2是x2+ax+b=0的两个实数根，
∴-1+2=-a，-1×2=b，
解得a=-1，b=-2．
∴a+b=-3．
故选：A．
点评：本题考查了一元二次不等式的解集与相应的一元二次方程的实数根之间的关系，属于基础题．
练习册系列答案
培优口算题卡系列答案
开心口算题卡系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
关于平面向量
，
，
有下列三个命题：
①若
•
=
•
，则
=
②若
=（1，k）
=（-2，6），
⊥
则k=
③非零向量
和
满足|
|=|
|=|
-
|，则
与
+
的夹角为60°，
其中真命题的序号为（ ）
| a |
| b |
| c |
①若
| a |
| b |
| a |
| c |
| b |
| c |
②若
| a |
| b |
| a |
| b |
| 1 |
| 3 |
③非零向量
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| a |
| b |
其中真命题的序号为（ ）
| A、①② | B、② | C、②③ | D、①②③ |
若关于x的不等式a≤
x2-3x+4≤b的解集恰好是[a，b]，则b-a的值为（ ）
| 3 |
| 4 |
| A、1 | B、2 | C、3 | D、4 |
在△ABC中，AB=1，BC=2，B=60°，M为AC中点，则
•
的值为（ ）
| AB |
| AM |
| A、0 | ||
| B、1 | ||
C、
| ||
| D、2 |
函数f（x）=2sin（
x+
）是（ ）
| 2 |
| 3 |
| 15π |
| 2 |
| A、周期为3π的偶函数 | ||
| B、周期为3π的奇函数 | ||
C、周期为
| ||
D、周期为
|
已知函数f（x）=
的对称中心是（3，-1），则实数a的值为（ ）
| a-x |
| x-a-1 |
| A、2 | B、3 | C、-2 | D、-4 |
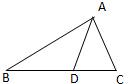如图，已知| AB |
| a |
| AC |
| b |
| BD |
| DC |
| a |
| b |
| AD |
| AD |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
如果{an}为递增数列（n∈N*），则{an}的通项公式可以为（ ）
| A、an=n2-n-2 | ||
| B、an=-2n+3 | ||
C、an=
| ||
| D、an=n-log2n |
点P是函数f（x）=cosωx（其中ω＞0）的图象C的一个对称中心，若点P到图象C的对称轴的距离最小值是π，则ω为（ ）
A、
| ||
| B、4 | ||
| C、2 | ||
D、
|