题目内容
点P是函数f(x)=cosωx(其中ω>0)的图象C的一个对称中心,若点P到图象C的对称轴的距离最小值是π,则ω为( )
A、
| ||
| B、4 | ||
| C、2 | ||
D、
|
考点:函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:首先根据点P是函数f(x)=cosωx(其中ω>0)的图象C的一个对称中心,点P到图象C的对称轴的距离最小值是π,说明P到图象C的对称轴的距离占
,建立关系求得周期,进一步求得ω的值.
| T |
| 4 |
解答:
解:∵点P是函数f(x)=cosωx(其中ω>0)的图象C的一个对称中心,点P到图象C的对称轴的距离最小值是π
∴
=π 即:T=4π
∴根据ω=
=
故选:A
∴
| T |
| 4 |
∴根据ω=
| 2π |
| T |
| 1 |
| 2 |
故选:A
点评:本题考查的知识点:余弦型函数的图象和性质以及周期公式,属基础题

练习册系列答案
相关题目
不等式x2+ax+b≤0的解集是[-1,2],则a+b的值是( )
| A、-3 | B、-1 | C、1 | D、3 |
设a>b>c,ac<0,则下列不等式不一定成立的是( )
| A、ab>ac |
| B、c(b-a)>0 |
| C、cb2<ab2 |
| D、ac(a-c)<0 |
在区间(0,+∞)是减函数的是( )
| A、y=2x+1 | ||
| B、y=3x2+1 | ||
C、y=
| ||
| D、y=2x |
设函数f(x)=-x+2,x∈[-5,5],若从区间[-5,5]内随机选取一个实数x0,则所选取的实数x0满足f(x0)≤0的概率为( )
| A、0.5 | B、0.4 |
| C、0.3 | D、0.2 |
已知等比数列{an}的公比q=-2,则
等于( )
| a1a3a5a7 |
| a2a4a6a8 |
A、-
| ||
B、
| ||
C、
| ||
D、-
|
若角α的终边经过点P(-1,2),则sinα等于( )
A、-
| ||||
B、
| ||||
C、
| ||||
D、-
|
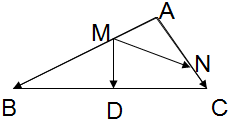 如图:在△ABC中,D为BC中点,AM=
如图:在△ABC中,D为BC中点,AM=