题目内容
函数f（x）=2sin（
x+
）是（ ）
| 2 |
| 3 |
| 15π |
| 2 |
| A、周期为3π的偶函数 | ||
| B、周期为3π的奇函数 | ||
C、周期为
| ||
D、周期为
|
考点：三角函数的周期性及其求法,正弦函数的对称性
专题：三角函数的图像与性质
分析：根据诱导公式化简函数解析式，再得到函数的奇偶性、周期．
解答：
解：f（x）=2sin（
x+
）=2sin（7π+
+
x）
=-2sin（
+
x）=-2cos（
x），
所以函数式偶函数，且周期T=
=3π，
故选：A．
| 2 |
| 3 |
| 15π |
| 2 |
| π |
| 2 |
| 2 |
| 3 |
=-2sin（
| π |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
所以函数式偶函数，且周期T=
| 2π | ||
|
故选：A．
点评：本题考查诱导公式，三角函数的奇偶性及周期的求法，注意三角函数值的符号．
练习册系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
函数f（x）=
的定义域为（ ）
| lnx+1 | ||
|
| A、（-1，+∞） |
| B、（-∞，1） |
| C、（0，1） |
| D、（-1，1] |
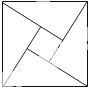2002年8月，在北京召开的国际数学家大会会标如图所示，会标是以我国古代数学家赵爽的弦图为基础设计的．弦图是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形，若直角三角形中较小的锐角为θ，大正方形的面积是1，小正方形的面积是| 1 |
| 25 |
| A、1 | ||
B、-
| ||
C、
| ||
D、-
|
函数y=cosωx（ω＞0）在区间[0，1）上至少出现2次最大值，至多出现3次最大值，则ω的取值范围是（ ）
| A、2π≤ω≤4π |
| B、2π＜ω≤4π |
| C、2π＜ω≤6π |
| D、2π＜ω＜6π |
设（x，y）在映射f下的象是（x+y，x-y），则象（1，2）的原象是（ ）
| A、（3，1） | ||||
B、（
| ||||
| C、（-1，3） | ||||
D、（-
|
不等式x2+ax+b≤0的解集是[-1，2]，则a+b的值是（ ）
| A、-3 | B、-1 | C、1 | D、3 |
下列函数是在（0，1）上为减函数的是（ ）
| A、y=x2 |
| B、y=x+1 |
| C、y=sinx |
| D、y=cosx |
正整数集合Ak中的最小元素为1，最大元素为2010，并且各元素可以从小到大排列成一个公差为k的等差数列，则并集A7∪A41中的元素个数为（ ）
| A、300 | B、310 |
| C、330 | D、360 |
设函数f（x）=-x+2，x∈[-5，5]，若从区间[-5，5]内随机选取一个实数x0，则所选取的实数x0满足f（x0）≤0的概率为（ ）
| A、0.5 | B、0.4 |
| C、0.3 | D、0.2 |