题目内容
若关于x的不等式a≤
x2-3x+4≤b的解集恰好是[a,b],则b-a的值为( )
| 3 |
| 4 |
| A、1 | B、2 | C、3 | D、4 |
考点:一元二次不等式的解法
专题:函数思想,函数的性质及应用
分析:设f(x)=
x2-3x+4,其函数图象是抛物线,画两条与x轴平行的直线y=a和y=b,如果两直线与抛物线有两个交点,得到解集应该是两个区间;此不等式的解集为一个区间,所以两直线与抛物线不可能有两个交点,所以直线y=a应该与抛物线只有一个或没有交点,所以a小于或等于抛物线的最小值且a与b所对应的函数值相等且都等于b,利用f(b)=b求出b的值,由抛物线的对称轴求出a的值,从而求出a+b的值.
| 3 |
| 4 |
解答:
解:设f(x)=
x2-3x+4,当x=-
=2时,f(x)min=1,
由题意知a≤1,且f(a)=f(b)=b,a<b;
由f(b)=b得
b2-3b+4=b,
解得b=
(舍去),或b=4,
∴b=4;
∵抛物线的对称轴为x=2,
∴a=0;
∴b-a=4.
故选:D.
| 3 |
| 4 |
| -3 | ||
2×
|
由题意知a≤1,且f(a)=f(b)=b,a<b;
由f(b)=b得
| 3 |
| 4 |
解得b=
| 4 |
| 3 |
∴b=4;
∵抛物线的对称轴为x=2,
∴a=0;
∴b-a=4.
故选:D.
点评:本题考查了二次函数的图象与性质的应用问题,解题时应灵活应用函数的思想解决实际问题,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知cosα=-
,则sin(30°+α)+sin(30°-α)的值为( )
| 1 |
| 2 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
f(x)=x3+bx2+cx+d的导函数f′(x)的图象关于直线x=2对称,则b的值为( )
| A、-3 | B、3 | C、1 | D、-6 |
如图,阴影部分表示的集合是( )


| A、A∪B |
| B、A∩B |
| C、?AB |
| D、∅ |
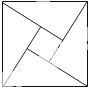 2002年8月,在北京召开的国际数学家大会会标如图所示,会标是以我国古代数学家赵爽的弦图为基础设计的.弦图是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形,若直角三角形中较小的锐角为θ,大正方形的面积是1,小正方形的面积是
2002年8月,在北京召开的国际数学家大会会标如图所示,会标是以我国古代数学家赵爽的弦图为基础设计的.弦图是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形,若直角三角形中较小的锐角为θ,大正方形的面积是1,小正方形的面积是| 1 |
| 25 |
| A、1 | ||
B、-
| ||
C、
| ||
D、-
|
设f(x),g(x)分别是定义在R上的奇函数和偶函数.当x<0时,f′(x)g(x)+f(x)g′(x)>0,且g(-3)=0,则不等式f(x)g(x)>0的解集是( )
| A、(-3,0)∪(0,3) |
| B、(-3,0)∪(3,+∞) |
| C、(-∞,-3)∪(3,+∞) |
| D、(-∞,-3)∪(0,3) |
函数y=cosωx(ω>0)在区间[0,1)上至少出现2次最大值,至多出现3次最大值,则ω的取值范围是( )
| A、2π≤ω≤4π |
| B、2π<ω≤4π |
| C、2π<ω≤6π |
| D、2π<ω<6π |
不等式x2+ax+b≤0的解集是[-1,2],则a+b的值是( )
| A、-3 | B、-1 | C、1 | D、3 |
设a>b>c,ac<0,则下列不等式不一定成立的是( )
| A、ab>ac |
| B、c(b-a)>0 |
| C、cb2<ab2 |
| D、ac(a-c)<0 |