题目内容
已知函数f(x)=xlnx+ax(a∈R).
(Ⅰ)当a=0,求f(x)的最小值;
(Ⅱ)若函数g(x)=f(x)+lnx在区间[1,+∞)上为增函数,求实数a的取值范围;
(Ⅲ)过点P(1,-3)恰好能作函数y=f(x)图象的两条切线,并且两切线的倾斜角互补,求实数a的取值范围.
(Ⅰ)当a=0,求f(x)的最小值;
(Ⅱ)若函数g(x)=f(x)+lnx在区间[1,+∞)上为增函数,求实数a的取值范围;
(Ⅲ)过点P(1,-3)恰好能作函数y=f(x)图象的两条切线,并且两切线的倾斜角互补,求实数a的取值范围.
考点:利用导数研究曲线上某点切线方程
专题:综合题,导数的综合应用
分析:(Ⅰ)求导函数,确定函数的单调性,即可求f(x)的最小值;
(Ⅱ)函数g(x)在区间[1,+∞)上为增函数,可得当x∈[1,+∞)时g'(x)≥0,即lnx+
≥-(a+1)在[1,+∞)上恒成立,求出左边的最小值,即可求实数a的取值范围;
(Ⅲ)求出函数y=f(x)在A,B处的切线方程,利用过点P(1,-3),两切线的倾斜角互补,建立方程组,即可求实数a的取值范围.
(Ⅱ)函数g(x)在区间[1,+∞)上为增函数,可得当x∈[1,+∞)时g'(x)≥0,即lnx+
| 1 |
| x |
(Ⅲ)求出函数y=f(x)在A,B处的切线方程,利用过点P(1,-3),两切线的倾斜角互补,建立方程组,即可求实数a的取值范围.
解答:
解:(I)f(x)的定义域为(0,+∞)f′(x)=lnx+1,令f′(x)=0,得:x=
,…(1分)
当x∈(0,+∞)时,f'(x),f(x)的变化的情况如下:
…(3分)
∴f(x)的最小值是f(
)=-
.…(4分)
(Ⅱ)由题意得:g′(x)=lnx+a+1+
…(5分)
∵函数g(x)在区间[1,+∞)上为增函数,
∴当x∈[1,+∞)时g'(x)≥0,即lnx+
≥-(a+1)在[1,+∞)上恒成立,
∴h(x)=lnx+
,…(7分)
∴h′(x)=
-
=
,
∴h(x)=lnx+
在[1,+∞)上递增,
∴-(a+1)≤h(1)=1,
∴a≥-2…(10分)
(Ⅲ)设两切点A(x1,f(x1)),B(x2,f(x2)),f'(x)=lnx+1+a
则函数y=f(x)在A,B处的切线方程分别为y=(lnx1+1+a)(x-x1)+x1lnx1+ax1=(lnx1+1+a)x-x1,
∴y=(lnx2+1+a)(x-x2)+x2lnx2+ax2=(lnx2+1+a)x-x2
且lnx1+1+a+lnx2+1+a=0
即
也即
即x1,x2是方程t2-6t+e-2(a+1)=0的两个正根,
∴△=36-4e-2(a+1)>0,
∴a>-1-ln3…(15分)
| 1 |
| e |
当x∈(0,+∞)时,f'(x),f(x)的变化的情况如下:
| x | (0,
|
|
(
| ||||||
| f'(x) | - | 0 | + | ||||||
| f(x) | 极小值 |
∴f(x)的最小值是f(
| 1 |
| e |
| 1 |
| e |
(Ⅱ)由题意得:g′(x)=lnx+a+1+
| 1 |
| x |
∵函数g(x)在区间[1,+∞)上为增函数,
∴当x∈[1,+∞)时g'(x)≥0,即lnx+
| 1 |
| x |
∴h(x)=lnx+
| 1 |
| x |
∴h′(x)=
| 1 |
| x |
| 1 |
| x2 |
| x-1 |
| x2 |
∴h(x)=lnx+
| 1 |
| x |
∴-(a+1)≤h(1)=1,
∴a≥-2…(10分)
(Ⅲ)设两切点A(x1,f(x1)),B(x2,f(x2)),f'(x)=lnx+1+a
则函数y=f(x)在A,B处的切线方程分别为y=(lnx1+1+a)(x-x1)+x1lnx1+ax1=(lnx1+1+a)x-x1,
∴y=(lnx2+1+a)(x-x2)+x2lnx2+ax2=(lnx2+1+a)x-x2
且lnx1+1+a+lnx2+1+a=0
即
|
|
即x1,x2是方程t2-6t+e-2(a+1)=0的两个正根,
∴△=36-4e-2(a+1)>0,
∴a>-1-ln3…(15分)
点评:本题考查函数的单调性与最值,考查恒成立问题,考查分离参数法的运用,考查导数的几何意义,正确求导是关键.

练习册系列答案
相关题目
直线y=kx+b与圆(x-1)2+(y-2)2=5有公共点的一个充分不必要条件为( )
| A、b≤4 | B、b≥0 |
| C、-4≤b≤4 | D、0≤b≤4 |
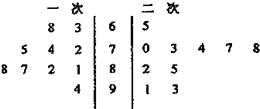 如图是某同学一学期两次考试成绩的茎叶图,现从该同学两次考试成绩中各取一科成绩,则这两科成绩都在80分以上的概率为( )
如图是某同学一学期两次考试成绩的茎叶图,现从该同学两次考试成绩中各取一科成绩,则这两科成绩都在80分以上的概率为( )A、
| ||
B、
| ||
C、
| ||
D、
|