题目内容
若在不等式组
所确定的平面区域内任取一点P(x,y),则点P的坐标满足x2+y2≤2的概率是 .
|
考点:几何概型
专题:概率与统计
分析:组成不等式组对应的平面区域,利用几何概型的概率公式即可得到结论.
解答:
 解:不等式组
解:不等式组
对应的平面区域为三角形OAB对应的面积为
×2×1=1,
x2+y2≤2表示的区域为半径为
的圆在三角形OAB内部的部分,对应的面积为
×π×(
)2=
,
∴根据几何概型的概率公式,得到所求对应概率公式为
.
故答案为:
.
 解:不等式组
解:不等式组
|
| 1 |
| 2 |
x2+y2≤2表示的区域为半径为
| 2 |
| 1 |
| 8 |
| 2 |
| π |
| 4 |
∴根据几何概型的概率公式,得到所求对应概率公式为
| π |
| 4 |
故答案为:
| π |
| 4 |
点评:本题主要考查几何概型的概率公式,利用二元一次不等式组表示平面区域求出对应的面积是解决本题的关键.

练习册系列答案
相关题目
已知x,y满足约束条件
,则目标函数z=2x-3y的最大值( )
|
| A、2 | B、3 | C、4 | D、5 |
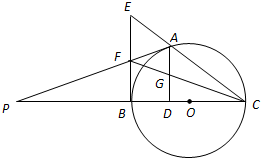 如图,A是以BC为直径的⊙O上一点,AD⊥BC于点D,过点B作⊙O的切线,与CA的延长线相交于点E,G是AD的中点,连结CG并延长与BE相交于点F,延长AF与CB的延长线相交于点P.
如图,A是以BC为直径的⊙O上一点,AD⊥BC于点D,过点B作⊙O的切线,与CA的延长线相交于点E,G是AD的中点,连结CG并延长与BE相交于点F,延长AF与CB的延长线相交于点P.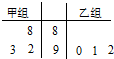 甲、乙两组各有三名同学,他们在一次测验中的成绩的茎叶图如图所示,如果分别从甲、乙两组中各随机挑选一名同学,则这两名同学成绩相同的概率是
甲、乙两组各有三名同学,他们在一次测验中的成绩的茎叶图如图所示,如果分别从甲、乙两组中各随机挑选一名同学,则这两名同学成绩相同的概率是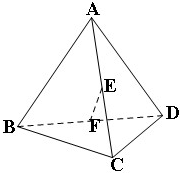 如图是将边长为2,有一内角为60°的菱形ABCD沿较短对角线BD折成四面体ABCD,点E、F分别为AC、BD的中点,则下列命题中正确的是
如图是将边长为2,有一内角为60°的菱形ABCD沿较短对角线BD折成四面体ABCD,点E、F分别为AC、BD的中点,则下列命题中正确的是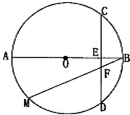 如图,AB为半径为2的圆O的直径,CD为垂直于AB的一条弦,垂足为E,弦BM与CD交于点F.则AC2+BF•BM=
如图,AB为半径为2的圆O的直径,CD为垂直于AB的一条弦,垂足为E,弦BM与CD交于点F.则AC2+BF•BM= 某校高三第一次模考中,对总分450分(含450分)以上的成绩进行统计,其频率分布直方图如图所示,若650~700分数段的人数为90,则500~550分数段的人数为
某校高三第一次模考中,对总分450分(含450分)以上的成绩进行统计,其频率分布直方图如图所示,若650~700分数段的人数为90,则500~550分数段的人数为