题目内容
2.已知f($\frac{x+1}{x}$)=$\frac{2x+1}{{x}^{2}}$,则( )| A. | f(x)=x2+1(x≠0) | B. | f(x)=x2+1(x≠1) | C. | f(x)=x2-1(x≠1) | D. | f(x)=x2-1(x≠0) |
分析 由f($\frac{x+1}{x}$)=$\frac{2x+1}{{x}^{2}}$,变形为$f(\frac{x+1}{x})$=$(\frac{x+1}{x})^{2}$-1,即可得出.
解答 解:由$f({\frac{x+1}{x}})=\frac{2x+1}{x^2}=\frac{{{x^2}+2x+1}}{x^2}-1={({\frac{x+1}{x}})^2}-1$,
得f(x)=x2-1,
又∵$\frac{x+1}{x}$≠1,
∴f(x)=x2-1的x≠1.
故选:C.
点评 本题考查了函数的解析式求法,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.直线l垂直于直线y=x+1,原点O到l的距离为1,且l与y轴正半轴有交点,则直线l的方程是( )
| A. | x+y-$\sqrt{2}$=0 | B. | x+y+1=0 | C. | x+y-1=0 | D. | x+y+$\sqrt{2}$=0 |
7.设a∈R,则1+a+a2+…+an的值为( )
| A. | $\frac{1-{a}^{n}}{1-a}$ | B. | $\frac{1-{a}^{n+1}}{1-a}$ | C. | $\frac{1-{a}^{n+1}}{1-a}$或n+1 | D. | 以上都不是 |
14.设点P为有公共焦点F1、F2的椭圆M和双曲线Г的一个交点,且cos∠F1PF2=$\frac{3}{5}$,椭圆M的离心率为e1,双曲线Г的离心率为e2.若e2=2e1,则e1=( )
| A. | $\frac{\sqrt{7}}{5}$ | B. | $\frac{\sqrt{7}}{4}$ | C. | $\frac{\sqrt{10}}{5}$ | D. | $\frac{\sqrt{10}}{4}$ |
14.如图为一几何体的三视图,其中这三个视图完全一样,则该几何体的表面积为( )
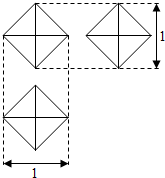

| A. | $\sqrt{3}$ | B. | 2$\sqrt{2}$ | C. | 4 | D. | 6 |
11.执行如图所示的程序框图,如果输入的x,t均为2,则输出的M等于( )
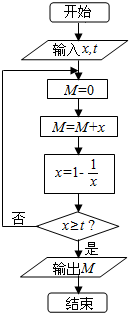

| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{5}{2}$ | D. | $\frac{7}{2}$ |