题目内容
已知f(x)是定义在R上的偶函数,g(x)是定义在R上的奇函数,且g(x)=f(x-1),则f(2013)+f(2015)的值为( )
| A、-1 | B、1 | C、0 | D、无法计算 |
考点:函数奇偶性的性质
专题:计算题,函数的性质及应用
分析:先由f(x)是定义在R上的偶函数得f(-x)=f(x),然后利用g(x)与f(x)的关系,以及g(x)的奇偶性,得f(x+1)+f(x-1)=0,从而得到要求的数值.
解答:
解:∵f(-x-1)=g(-x)=-g(x)=-f(x-1),又f(x)为偶函数
∴f(x+1)=f[-(x+1)]=f(-x-1),于是f(x+1)=-f(x-1)
∴f(x+1)+f(x-1)=0.
∴f(2013)+f(2015)=f(2014-1)+f(2014+1)=0,
故选:C.
∴f(x+1)=f[-(x+1)]=f(-x-1),于是f(x+1)=-f(x-1)
∴f(x+1)+f(x-1)=0.
∴f(2013)+f(2015)=f(2014-1)+f(2014+1)=0,
故选:C.
点评:本题考查了函数的奇偶性和周期性,考查了如何通过替代自变量的值求函数的周期,体现了数学转化思想,考查了学生的抽象思维能力,此题是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知复数z=
,则|z|=( )
| ||
(1-
|
| A、2 | ||||
B、
| ||||
C、
| ||||
D、
|
在区间[1,5]上任取一个数m,则函数y=x2-4x-2(0≤x≤m)的值域为[-6,-2]的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
集U={x|x≤1},A={x|-2≤x≤1},则∁UA=( )
| A、{x|x≤-2} |
| B、{x|x≤-2或x≥1} |
| C、{x|x<-2} |
| D、{x|x<-2或x>1} |
“a=1”是“关于x的方程x2-2x+a=0有实数根”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
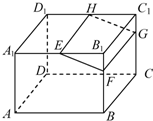 如图,在长方体ABCD-A1B1C1D1中,E,H分别是棱A1B1,D1C1上的点(点E与B1不重合),且EH∥A1D1,过EH的平面与棱BB1,CC1相交,交点分别为F,G.设AB=2AA1=2a,EF=a,B1E=2B1F.在长方体ABCD-A1B1C1D1内随机选取一点,则该点取自于几何体A1ABFE-D1DCGH内的概率为
如图,在长方体ABCD-A1B1C1D1中,E,H分别是棱A1B1,D1C1上的点(点E与B1不重合),且EH∥A1D1,过EH的平面与棱BB1,CC1相交,交点分别为F,G.设AB=2AA1=2a,EF=a,B1E=2B1F.在长方体ABCD-A1B1C1D1内随机选取一点,则该点取自于几何体A1ABFE-D1DCGH内的概率为