题目内容
函数y=
的周期是 ．
| 1+cos2x |
| sin2x |
考点：三角函数的周期性及其求法,二倍角的正弦,二倍角的余弦
专题：三角函数的求值
分析：直接利用二倍角公式化简函数的表达式，然后利用周期公式求解就．
解答：
解：函数y=
=
=
．
所以函数的周期为：π．
故答案为：π．
| 1+cos2x |
| sin2x |
| 1+2cos2x-1 |
| 2sinxcosx |
| 1 |
| tanx |
所以函数的周期为：π．
故答案为：π．
点评：本题考查三角函数的化简求值，三角函数的周期的求法，基本知识的考查．
练习册系列答案
导学全程练创优训练系列答案
相关题目
某单位安排2013年春节期间7天假期的值班情况，7个员工每人各值一天．已知某员工甲必须排在前两天，员工乙不能排在第一天，员工丙必须排在最后一天，则不同的值班顺序有（ ）
| A、120种 | B、216种 |
| C、720种 | D、540种 |
已知sinα=-
，且α是第四象限角，则tanα的值为（ ）
| 3 |
| 5 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
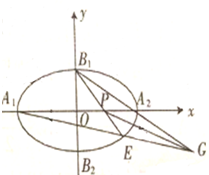已知焦点在x轴上的椭圆C的短轴长为2，离心率为
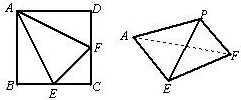正方形ABCD的边长为1，E、F分别为BC、CD的中点，沿AE、EF、AF折成四面体则四面体PAEF使B、C、D三点重合于P，则P到面AEF的距离为已知点P在定圆O的圆内或圆周上，动圆C过点P与定圆O相切，则动圆C的圆心轨迹可能是（ ）
| A、圆或椭圆成双曲线 |
| B、两条射线或圆或抛物线 |
| C、两条射线或圆或椭圆 |
| D、椭圆或双曲线或抛物线 |