题目内容
设锐角△ABC的内角A,B,C的对边分别为a,b,c,且ccosB+
bsinC=a.
(1)求角C的大小;
(2)若c=1,求a2+b2的取值范围.
| 3 |
(1)求角C的大小;
(2)若c=1,求a2+b2的取值范围.
考点:两角和与差的正弦函数,余弦定理
专题:解三角形
分析:(1)由条件利用正弦定理可得 sinCcosB+
sinBsinC=sinA,化简可得
sinBsinC=sinBcosC.求得tanC的值,可得C的值.
(2)再由余弦定理可得c2=1=a2+b2-
ab≥
(a2+b2),可得a2+b2≤4+2
.由三角形任意两边之和大于第三边以及基本不等式求得a2+b2>
,从而求得a2+b2的取值范围.
| 3 |
| 3 |
(2)再由余弦定理可得c2=1=a2+b2-
| 3 |
2-
| ||
| 2 |
| 3 |
| 1 |
| 2 |
解答:
解:(1)锐角△ABC中,∵ccosB+
bsinC=a,
∴由正弦定理可得:sinCcosB+
sinBsinC=sinA,
即sinCcosB+
sinBsinC=sin(B+C)=sinBcosC+cosBsinC,
即
sinBsinC=sinBcosC.
∵sinB≠0,∴tanC=
,C=
.
(2)∵a2+b2≥2ab,∴ab≤
,∴-
ab≥-
(a2+b2).
再由余弦定理可得c2=1=a2+b2-2ab•cosC=a2+b2-
ab≥
(a2+b2),
∴a2+b2≤
=
=4+2
.
由三角形任意两边之和大于第三边,可得a+b>c=1,
平方可得a2+b2+2ab>1,∴2(a2+b2)>1,∴a2+b2>
.
综上可得,a2+b2 ∈(
,4+2
].
| 3 |
∴由正弦定理可得:sinCcosB+
| 3 |
即sinCcosB+
| 3 |
即
| 3 |
∵sinB≠0,∴tanC=
| ||
| 3 |
| π |
| 6 |
(2)∵a2+b2≥2ab,∴ab≤
| a2+b2 |
| 2 |
| 3 |
| ||
| 2 |
再由余弦定理可得c2=1=a2+b2-2ab•cosC=a2+b2-
| 3 |
2-
| ||
| 2 |
∴a2+b2≤
| 2 | ||
2-
|
2(2+
| ||||
(2-
|
| 3 |
由三角形任意两边之和大于第三边,可得a+b>c=1,
平方可得a2+b2+2ab>1,∴2(a2+b2)>1,∴a2+b2>
| 1 |
| 2 |
综上可得,a2+b2 ∈(
| 1 |
| 2 |
| 3 |
点评:本题主要考查正弦定理、余弦定理、基本不等式的应用,属于中档题.

练习册系列答案
相关题目
执行如图所示的程序框图,若输出的S为4,则输入的x应为( )


| A、-2 | B、16 |
| C、-2或8 | D、-2或16 |
对任意两实数a,b,定义运算“*”:a*b=
,关于函数f(x)=e-x*ex-1给出下列四个结论:
①函数f(x)为偶函数;
②函数f(x)的最小值是
③函数f(x)在(0,+∞)上单调递增
④函数f(x)的图象与直线y=e(x+1)有公共点
其中正确结论的序号是( )
|
①函数f(x)为偶函数;
②函数f(x)的最小值是
| 1 | ||
|
③函数f(x)在(0,+∞)上单调递增
④函数f(x)的图象与直线y=e(x+1)有公共点
其中正确结论的序号是( )
| A、①③ | B、②③ | C、①④ | D、②④ |
(x-
y)8的展开式中x6y2项的系数是( )
| 2 |
| A、56 | B、-56 |
| C、28 | D、-28 |
已知某几何体的三视图如图所示,则该几何体的体积为( )
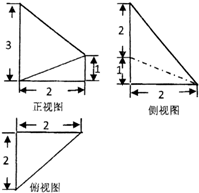

| A、8 | ||
B、
| ||
| C、4 | ||
| D、12 |
 学校或班级举行活动,通常需要张贴海报进行宣传.现让你设计一张如图所示的竖向张贴的海报,要求版心面积为128dm2,上、下两边各空2dm,左、右两边各空1dm.如何设计海报的尺寸,才能使四周空白面积最小?
学校或班级举行活动,通常需要张贴海报进行宣传.现让你设计一张如图所示的竖向张贴的海报,要求版心面积为128dm2,上、下两边各空2dm,左、右两边各空1dm.如何设计海报的尺寸,才能使四周空白面积最小?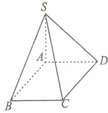 如图,在四棱锥S-ABCD中,底面ABCD是菱形,SA⊥平面ABCD
如图,在四棱锥S-ABCD中,底面ABCD是菱形,SA⊥平面ABCD