题目内容
已知函数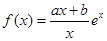 (
(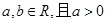 ).
).
(1)若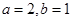 ,求函数
,求函数 的极值;
的极值;
(2)设 .
.
① 当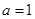 时,对任意
时,对任意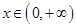 ,都有
,都有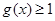 成立,求
成立,求 的最大值;
的最大值;
② 设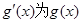 的导函数.若存在
的导函数.若存在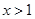 ,使
,使 成立,求
成立,求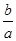 的取值范围.
的取值范围.
(1)参考解析; (2)①-1-e-1,②(-1,+∞)
解析试题分析:(1)由函数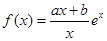 (
(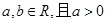 ),且
),且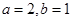 ,所以对函数
,所以对函数 求导,根据导函数的正负性可得到结论
求导,根据导函数的正负性可得到结论
(2)①当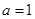 时,对任意
时,对任意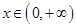 ,都有
,都有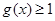 成立,即
成立,即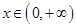 时,
时,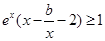 恒成立. 由此可以通过分离变量或直接求函数的最值求得结果,有分离变量可得b≤x2-2x-
恒成立. 由此可以通过分离变量或直接求函数的最值求得结果,有分离变量可得b≤x2-2x-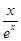 在x∈(0,+∞)上恒成立.通过求函数h(x)=x2-2x-
在x∈(0,+∞)上恒成立.通过求函数h(x)=x2-2x-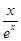 (x>0)的最小值即可得到结论.
(x>0)的最小值即可得到结论.
②若存在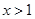 ,使
,使 .通过表示
.通过表示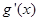 即可得到
即可得到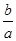 =
=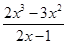 ,所以求出函数u(x)=
,所以求出函数u(x)=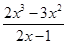 (x>1)的单调性即可得到结论.
(x>1)的单调性即可得到结论.
(1)当a=2,b=1时,f (x)=(2+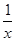 )ex,定义域为(-∞,0)∪(0,+∞).
)ex,定义域为(-∞,0)∪(0,+∞).
所以f ′(x)=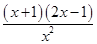 ex. 2分
ex. 2分
令f ′(x)=0,得x1=-1,x2=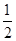 ,列表
,列表x (-∞,-1) -1 (-1,0) (0, 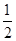 )
)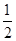
( 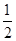 ,+∞)
,+∞)f ′(x) 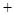

- - 
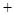
f (x) ↗ 极大值 ↘ ↘ 极小值 ↗
由表知f (x)的极大值是f (-1)=e-1,f (x)的极小值是f (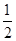 )=4
)=4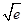 . 4分
. 4分
(2)① 因为g (x)=(ax-a)ex-f (x)=(ax-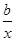 -2a)ex,
-2a)ex,
当a=1时,g (x)=(x-
练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
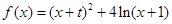 的图象在点
的图象在点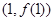 处的切线垂直于
处的切线垂直于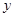 轴.
轴.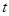 的值;
的值;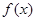 的极值.
的极值.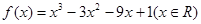 .
.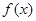 在点
在点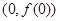 处的切线方程;
处的切线方程;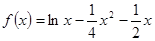 .
.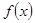 的单调区间和极值;
的单调区间和极值; ,当
,当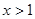 时,
时,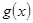 在区间
在区间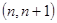 内存在极值,求整数
内存在极值,求整数 的值.
的值.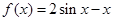 ,
,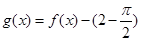 .
.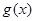 在
在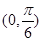 内和在
内和在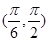 内的零点情况.
内的零点情况.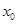 是
是 在
在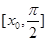 上的最值.
上的最值.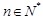 恒有
恒有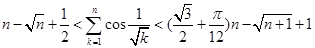 .[来
.[来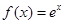 ,
,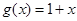 .
.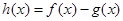 的最小值;
的最小值;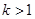 ,证明:当
,证明:当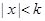 时,
时,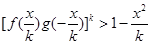 .
.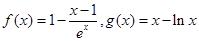 .
.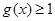 ;
;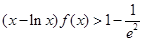 .
.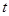 表示时间,以月为单位,年初为起点,根据历年数据,某水库的蓄水量(单位:亿立方米)关于
表示时间,以月为单位,年初为起点,根据历年数据,某水库的蓄水量(单位:亿立方米)关于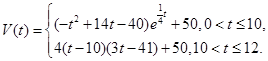
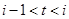 表示第1月份(
表示第1月份(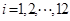 ),同一年内哪几个月份是枯水期?
),同一年内哪几个月份是枯水期?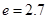 计算).
计算).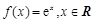 .
. 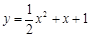 有唯一公共点.
有唯一公共点. 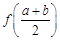 与
与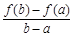 的大小, 并说明理由.
的大小, 并说明理由.