题目内容
设函数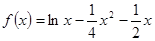 .
.
(1)求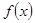 的单调区间和极值;
的单调区间和极值;
(2)若 ,当
,当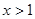 时,
时,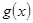 在区间
在区间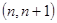 内存在极值,求整数
内存在极值,求整数 的值.
的值.
(1)详见解析;(2)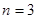 .
.
解析试题分析:(1)此问为导数的基础题型,先求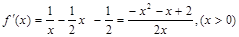 ,令
,令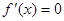 ,求极值点,然后解
,求极值点,然后解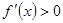 与
与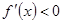 ,列出
,列出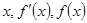 的变化表格,从而很容易确定单调区间,以及极值;
的变化表格,从而很容易确定单调区间,以及极值;
(2)代入得到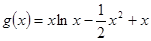 ,先求
,先求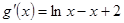 ,从
,从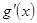 无法确定函数的极值点,所以求其二阶导数,令
无法确定函数的极值点,所以求其二阶导数,令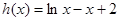 ,
, 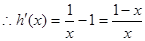 ,当
,当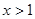 时,
时,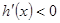 恒成立,
恒成立,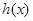 在
在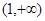 为单调递减函数,那么
为单调递减函数,那么 的值为极值点,因为是正整数,所以从
的值为极值点,因为是正整数,所以从 开始判定符号,
开始判定符号,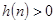 ,
,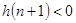 ,即为极值点的区间.
,即为极值点的区间.
(1)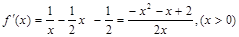 令
令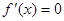 ,解得
,解得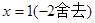 ,
,
根据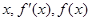 的变化情况列出表格:
的变化情况列出表格:
(0,1) 1 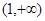
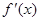
+ 0 _ 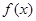
递增 极大值 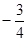
递减
由上表可知函数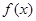 的单调增区间为(0,1),递减区间为
的单调增区间为(0,1),递减区间为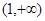 ,
,
在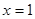 处取得极大值
处取得极大值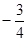 ,无极小值.. 5分
,无极小值.. 5分
(2)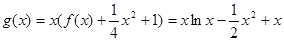 ,
,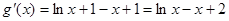 ,
,
令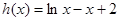 ,
, 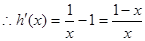 ,
,
因为 恒成立,所以
恒成立,所以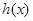 在
在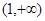 为单调递减函数,
为单调递减函数,
因为
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
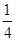 x+3垂直,求切点坐标与切线的方程.
x+3垂直,求切点坐标与切线的方程.
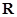 ).
).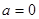 时,求函数
时,求函数 在点
在点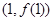 处的切线方程;
处的切线方程; 在
在 上是减函数,求实数
上是减函数,求实数 的取值范围;
的取值范围; 是否存在实数
是否存在实数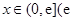 是自然对数的底)时,函数
是自然对数的底)时,函数 的最小值是
的最小值是 .若存在,求出
.若存在,求出 ,
, .
. 在
在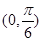 内和在
内和在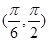 内的零点情况.
内的零点情况.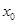 是
是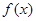 在
在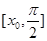 上的最值.
上的最值.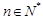 恒有
恒有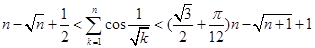 .[来
.[来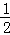 对称,且f′(1)=0
对称,且f′(1)=0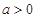 ,函数
,函数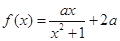 ,
,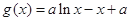 .
. 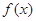 的单调区间;
的单调区间;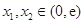 ,都有
,都有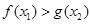 .
.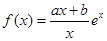 (
(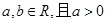 ).
).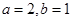 ,求函数
,求函数 的极值;
的极值; .
.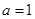 时,对任意
时,对任意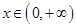 ,都有
,都有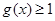 成立,求
成立,求 的最大值;
的最大值;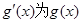 的导函数.若存在
的导函数.若存在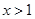 ,使
,使 成立,求
成立,求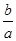 的取值范围.
的取值范围. ,其中
,其中 .
. ,求函数
,求函数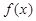 的极值;
的极值;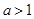 时,试确定函数
时,试确定函数 ,其中e为自然对数的底数.
,其中e为自然对数的底数.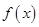 是增函数,求实数
是增函数,求实数 的取值范围;
的取值范围; 时,求函数
时,求函数 上的最小值;
上的最小值; .
.