题目内容
8.某公司的班车分别在7:30,8:30发车,小明在7:50至8:30之间到达发车站乘坐班车,且到达发车站的时刻是随机的,则他等车时间不超过15分钟的概率是( )| A. | $\frac{1}{3}$ | B. | $\frac{3}{8}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{8}$ |
分析 求出小明等车时间不超过15分钟的时间长度,代入几何概型概率计算公式,可得答案.
解答 解:设小明到达时间为y,
当y在8:15至8:30时,小明等车时间不超过15分钟,
故P=$\frac{15}{40}$=$\frac{3}{8}$,
故选:B.
点评 本题考查的知识点是几何概型,难度不大,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.甲、乙两企业根据赛事组委会要求为获奖者定做某工艺品作为奖品,其中一等奖奖品3件,二等奖奖品6件;制作一等奖、二等奖所用原料完全相同,但工艺不同,故价格有所差异.甲厂收费便宜,但原料有限,最多只能制作4件奖品,乙厂原料充足,但收费较贵,其具体收费如表所示,则组委会定做该工艺品的费用总和最低为4900元.
| 奖品 缴费(无/件) 工厂 | 一等奖奖品 | 二等奖奖品 |
| 甲 | 500 | 400 |
| 乙 | 800 | 600 |
17.函数y=f(x)导函数的图象如图所示,则下列说法错误的是( )
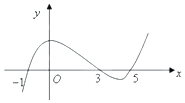

| A. | (-1,3)为函数y=f(x)的递增区间 | B. | (3,5)为函数y=f(x)的递减区间 | ||
| C. | 函数y=f(x)在x=0处取得极大值 | D. | 函数y=f(x)在x=5处取得极小值 |
9.“m>n>0”是方程mx2+ny2=1表示椭圆的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
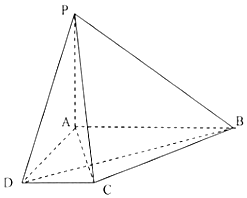 如图,四棱锥P-ABCD中,底面ABCD为直角梯形,∠BAD=∠ADC=90°,AP=AD=2CD=1,AB=2,PA⊥平面ABCD.
如图,四棱锥P-ABCD中,底面ABCD为直角梯形,∠BAD=∠ADC=90°,AP=AD=2CD=1,AB=2,PA⊥平面ABCD.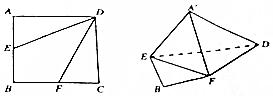 如图,在边长为4的正方形ABCD中,将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于点A′.
如图,在边长为4的正方形ABCD中,将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于点A′.