题目内容
10.已知函数f(x)=|x-a|-|x+1|,且f(x)不恒为0.(1)若f(x)为奇函数,求a值;
(2)若当x∈[-1,2]时,f(x)≤3恒成立,求实数a的取值范围.
分析 (1)由奇函数的性质可得f(0)=0,结合条件可得a=1,检验即可;
(2)由题意可得|x-a|≤4+x在x∈[-1,2]时恒成立.即有-4-x≤x-a≤x+4在x∈[-1,2]时恒成立,运用参数分离和一次函数的单调性,可得最值,进而得到a的范围.
解答 解:(1)因为x∈R,若f(x)为奇函数,
则由f(0)=0,得|a|-1=0,
又f(x)不恒为0,得a=1.┉┉┉┉┉┉┉┉┉┉┉┉┉┉(4分)
此时f(-x)=|-x-1|-|-x+1|=-f(x),符合f(x)为奇函数,所以a=1.┉┉┉┉┉┉┉┉┉(5分)
(2)当x∈[-1,2]时,f(x)≤3恒成立,
即|x-a|≤4+x在x∈[-1,2]时恒成立.
故-4-x≤x-a≤x+4在x∈[-1,2]时恒成立,┉┉┉┉┉┉┉┉┉┉┉┉┉(8分)
即-4≤a≤(4+2x)min,x∈[-1,2].
而x∈[-1,2],(4+2x)min=2,所以a的范围是[-4,2].┉┉┉┉┉┉┉┉┉┉┉(10分)
点评 本题考查绝对值函数的性质和不等式恒成立问题解法,注意运用绝对值的含义和参数分离,求最值,考查转化思想,以及运算能力,属于中档题.

练习册系列答案
相关题目
1.函数f(x)=sinωx(?>0)的图象向右平移$\frac{π}{12}$个单位得到函数y=g(x)的图象,并且函数g(x)在区间[$\frac{π}{6}$,$\frac{π}{3}$]上单调递增,在区间[$\frac{π}{3},\frac{π}{2}$]上单调递减,则实数ω的值为( )
| A. | $\frac{7}{4}$ | B. | $\frac{3}{2}$ | C. | 2 | D. | $\frac{5}{4}$ |
5.设双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右顶点为A,右焦点为F(c,0),弦PQ过F且垂直于x轴,过点P、点Q分别作直线AQ、AP的垂线,两垂线交于点B,若B到直线PQ的距离小于2(a+c),则该双曲线离心率的取值范围是( )
| A. | (1,$\sqrt{3}$) | B. | ($\sqrt{3}$,+∞) | C. | (0,$\sqrt{3}$) | D. | (2,$\sqrt{3}$) |
2.某商场对A 商品近30 天的日销售量y(件)与时间t(天)的销售情况进行整理,得到如下数据经统计分析,日销售量y(件)与时间t(天)之间具有线性相关关系.
(1)请根据上表提供的数据,用最小二乘法原理求出 y 关于t的线性回归方程$\widehaty=bx+a$;
(2)已知A 商品近30 天内的销售价格Z(元)与时间t(天)的关系为:z=$\left\{\begin{array}{l}{t+20,(0<20,t∈N)}\\{-t+100,(20≤t≤30,t∈N)}\end{array}\right.$根据(1)中求出的线性回归方程,预测t为何值时,A 商品的日销售额最大.
(参考公式:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{t}_{i}{y}_{i}-n\overline{t}-\overline{y}}{\sum_{i=1}^{n}{{t}_{i}}^{2}-n{\overline{t}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{t}$)
| 时间(t) | 2 | 4 | 6 | 8 | 10 |
| 日销售量(y) | 38 | 37 | 32 | 33 | 30 |
(2)已知A 商品近30 天内的销售价格Z(元)与时间t(天)的关系为:z=$\left\{\begin{array}{l}{t+20,(0<20,t∈N)}\\{-t+100,(20≤t≤30,t∈N)}\end{array}\right.$根据(1)中求出的线性回归方程,预测t为何值时,A 商品的日销售额最大.
(参考公式:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{t}_{i}{y}_{i}-n\overline{t}-\overline{y}}{\sum_{i=1}^{n}{{t}_{i}}^{2}-n{\overline{t}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{t}$)
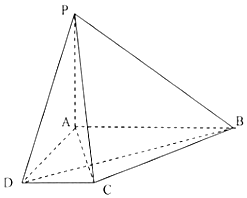 如图,四棱锥P-ABCD中,底面ABCD为直角梯形,∠BAD=∠ADC=90°,AP=AD=2CD=1,AB=2,PA⊥平面ABCD.
如图,四棱锥P-ABCD中,底面ABCD为直角梯形,∠BAD=∠ADC=90°,AP=AD=2CD=1,AB=2,PA⊥平面ABCD.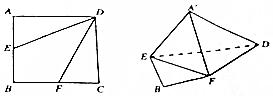 如图,在边长为4的正方形ABCD中,将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于点A′.
如图,在边长为4的正方形ABCD中,将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于点A′.