题目内容
11.设x,y满足约束条件$\left\{\begin{array}{l}x≥y\\ y≥4x-3\\ x≥0,y≥0\end{array}\right.$,若目标函数2z=2x+ny(n>0),z的最大值为2,则$y=tan({nx+\frac{π}{6}})$的图象向右平移$\frac{π}{6}$后的表达式为( )| A. | $y=tan({2x+\frac{π}{6}})$ | B. | $y=cot({x-\frac{π}{6}})$ | C. | $y=tan({2x-\frac{π}{6}})$ | D. | y=tan2x |
分析 画出约束条件的可行域,利用目标函数的最值求出n,然后利用三角函数的平移变换求解即可.
解答 解:作出可行域与目标函数基准线$y=-\frac{2}{n}x$,
由线性规划知识,可得当直线$z=x+\frac{n}{2}y$过点B(1,1)时,z取得最大值,即$1+\frac{n}{2}=2$,解得n=2;
则$y=tan({nx+\frac{π}{6}})$的图象向右平移$\frac{π}{6}$个单位后得到的解析式为$y=tan[{2({x-\frac{π}{6}})+\frac{π}{6}}]=tan({2x-\frac{π}{6}})$.
故选:C.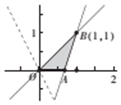
点评 本题考查线性规划的简单应用,三角函数的平移变换,考查转化思想以及计算能力.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
1.函数f(x)=sinωx(?>0)的图象向右平移$\frac{π}{12}$个单位得到函数y=g(x)的图象,并且函数g(x)在区间[$\frac{π}{6}$,$\frac{π}{3}$]上单调递增,在区间[$\frac{π}{3},\frac{π}{2}$]上单调递减,则实数ω的值为( )
| A. | $\frac{7}{4}$ | B. | $\frac{3}{2}$ | C. | 2 | D. | $\frac{5}{4}$ |
2.某商场对A 商品近30 天的日销售量y(件)与时间t(天)的销售情况进行整理,得到如下数据经统计分析,日销售量y(件)与时间t(天)之间具有线性相关关系.
(1)请根据上表提供的数据,用最小二乘法原理求出 y 关于t的线性回归方程$\widehaty=bx+a$;
(2)已知A 商品近30 天内的销售价格Z(元)与时间t(天)的关系为:z=$\left\{\begin{array}{l}{t+20,(0<20,t∈N)}\\{-t+100,(20≤t≤30,t∈N)}\end{array}\right.$根据(1)中求出的线性回归方程,预测t为何值时,A 商品的日销售额最大.
(参考公式:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{t}_{i}{y}_{i}-n\overline{t}-\overline{y}}{\sum_{i=1}^{n}{{t}_{i}}^{2}-n{\overline{t}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{t}$)
| 时间(t) | 2 | 4 | 6 | 8 | 10 |
| 日销售量(y) | 38 | 37 | 32 | 33 | 30 |
(2)已知A 商品近30 天内的销售价格Z(元)与时间t(天)的关系为:z=$\left\{\begin{array}{l}{t+20,(0<20,t∈N)}\\{-t+100,(20≤t≤30,t∈N)}\end{array}\right.$根据(1)中求出的线性回归方程,预测t为何值时,A 商品的日销售额最大.
(参考公式:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{t}_{i}{y}_{i}-n\overline{t}-\overline{y}}{\sum_{i=1}^{n}{{t}_{i}}^{2}-n{\overline{t}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{t}$)
12.已知m∈R,“方程ex+m-1=0有解”是“函数y=logmx在区间(0,+∞)为减函数”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
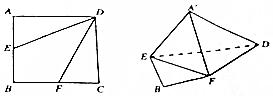 如图,在边长为4的正方形ABCD中,将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于点A′.
如图,在边长为4的正方形ABCD中,将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于点A′.